問 題
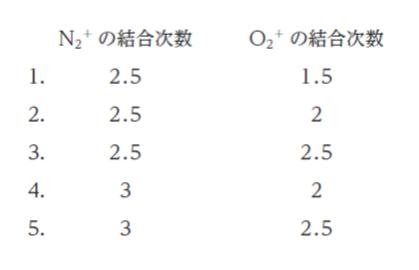
N2+ と O2+ それぞれの結合次数の組合せとして最も妥当なのはどれか。
解 説
結合次数は 「(結合性軌道の電子数-反結合性軌道の電子数) / 2」です。これは基礎知識です。
【N2+ の結合次数】
・窒素原子 N について考えます。
原子番号 7 で、電子数も 7 です。
軌道はエネルギーが低い方から 1s、2s、2px、2py、2pz です。
(1s)2 (2s)2 (2px)1 (2py)1 (2pz)1 と電子が入ります。
・次に N2 分子では、電子が計 14 個です。
1s 軌道同士、2s 軌道同士から、結合性軌道、反結合性軌道が 2 つずつ、計 4 つでき、電子が 2 つずつ入っていきます。4 × 2 = 8 個の電子については特に結合次数に影響しません。残りの電子 6 個が、どちらの軌道に何個入るかがポイントです。
2px,2py,2pz から それぞれ結合性軌道、反結合性軌道が 3 つずつできます。すると残りの電子 6 個はエネルギーの低い方から 2 個ずつ入っていき、結合性軌道の方がエネルギーが低いため「6全て結合性軌道」に 「各軌道に 電子 2 個ずつ」入ります。このため、結合次数は (6 – 0)/2 = 3 です。
本問では、ここから 1 個だけ電子が奪われた N2+ の結合次数が問われています。そのため、結合次数は 1/2 だけ N2 と比べて小さくなります。つまり、N2+ の結合次数は 3 – 0.5 = 2.5 です。正解は 1 ~ 3 です。
【O2+ の結合次数】
同様に O 原子 1 個 → O2 分子 から、1 個電子を取り除く という流れで考えます。
・酸素原子 O について
N に 1 個電子を追加すれば
(1s)2 (2s)2 (2px)2 (2py)1 (2pz)1 です。
※ 2px,2py,2pz は便宜的な名前なので、等価な軌道です。3 つの等価な軌道のうちどれかに残り 1 つの電子が入る ということを示しています。
・次に O2 分子では、電子が計 16 個です。
N2 に 2 個電子が追加なので、反結合性軌道に電子 2 個入ったものが O2 です。そのため、結合次数は (6 – 2)/2 = 2 です。
本問では、ここから 1 個だけ電子が奪われた O2+ の結合次数が問われています。そのため、結合次数は 1/2 だけ O2 と比べて大きくなります。つまり、O2+ の結合次数は 2 + 0.5 = 2.5 です。
以上より、正解は 3 です。
類題 R1 no24 等核ニ原子分子の結合次数、結合距離、磁気的性質
https://yaku-tik.com/yakugaku/km-r1-24/

コメント