問 題
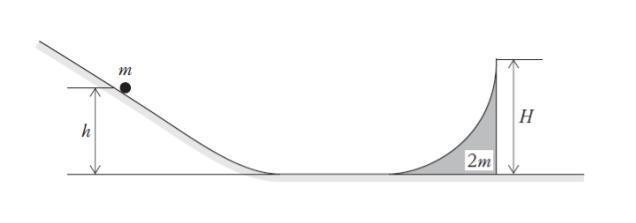
図のように、質量 2m、高さ H で、上面が滑らかな曲面である台が、斜面と水平面から成る滑らかな床の水平面の上に置かれている。水平面の左側には斜面があり、斜面、水平面及び台の曲面は滑らかにつながっている。
水平面からの高さが h (h < H) の斜面上において、質量 m の小球を静かに放した。すると、小球が台の曲面上で最高点に達し、このとき、台は右方向へ運動していた。水平面から小球が達した最高点までの高さとして最も妥当なのはどれか。
正解.4
解 説
まず、最下点での速さを求めます。力学的エネルギー保存則より、mgh = mv2/2 を解けば、v = √2gh…(1) です。
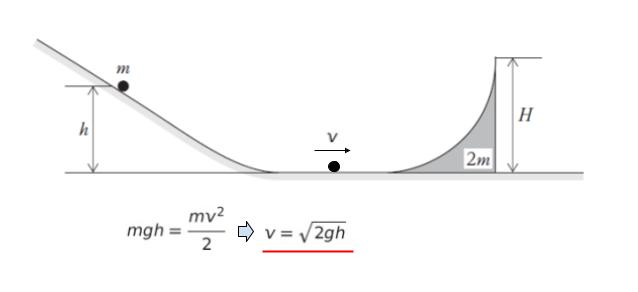
次に、台の曲面上で止まった時を考えます。その時の高さを H’ とします。先ほどの最下点で動いていたのは小球です。台の曲面上で小球が止まった時には台が動いています。この時の台の速さを V とおきます。
運動量保存則より
mv = mV + 2mV…(2) と表せます。
小球は見た目止まるのですが、台全体が動くので V で動いていると考えます。(2) を解けば V = v/3 です。
力学的エネルギー保存則より
mv2/2 = mgH’ + {3m × (v/3)2/2} です。H’ について解くと
H’ = v2/3g です。
すると (1) より v2/g = 2h なので
代入すればH’ = 2h/3 となります。
以上より、正解は 4 です。

コメント