国家公務員総合職（化学・生物・薬学）R5年 問13解説

　問 題　　　　　

 

 

 

 

 

　解 説　　　　　

・sin²θ + cos²θ = 1、sin,cos は「1 山の面積が 2」が基礎知識です。

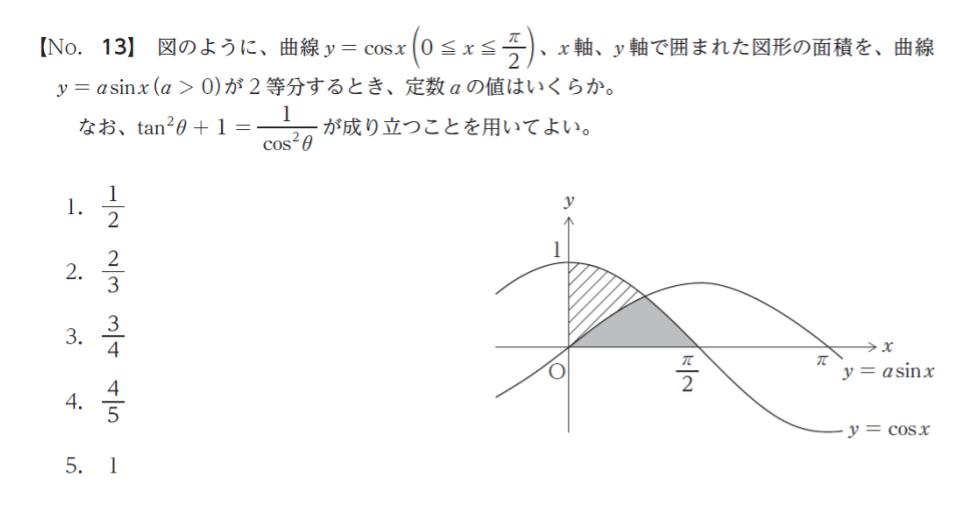
1 山の面積が 2 なので、x 軸、y 軸、y = cosx で囲まれる部分の面積は 1 です。y = asinx が 面積を 2 等分するので、それぞれの面積は 1/2 です。

選択肢を活用し、具体的に考えます。
a = 1/2 とすると、y = sinx/2 の最大値は 1/2 です。濃く塗られた部分の面積を三角形で近似して考えると、底辺 π/2、高さ 1/2 であっても、面積は π/8 にしかならず、小さすぎます。a = 1/2 ではありません。選択肢 1 は誤りです。

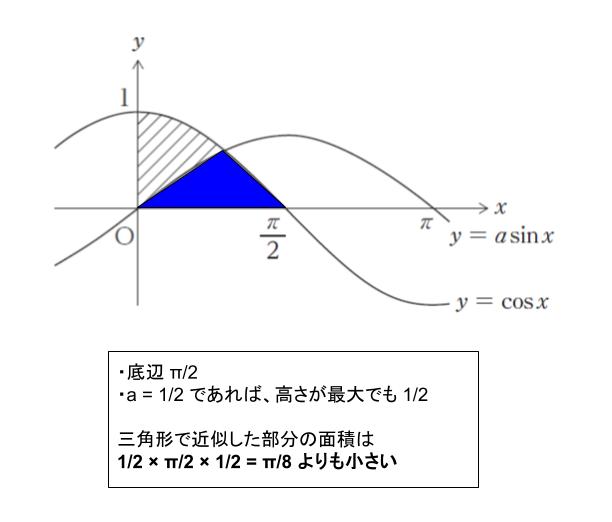
また、a = 1 の場合は、2 つの曲線が y = sin x と y = cos x なので交点が (π/4、√2/2) であることがすぐにわかります。三角形で近似して考えれば 底辺 π/2、高さ √2/2 ならば √2π/8 なので、1/2 を超えています。a = 1 も誤りです。選択肢 5 は誤りです。

残った 3 つの選択肢の中で真ん中の値で考えてみます。a = 3/4 とします。

交点を考えます。
(3/4) sinx = cosx  両辺ニ乗すれば
(9/16) sin²x = cos²x
(9/16) (1 – cos²x) = cos²x
(25/16)cos²x = 9/16
cos²x = 9/25
∴ cosx = 3/5 → sinx = 4/5 を満たす x が、交点の x 座標です。この x を α とおきます。

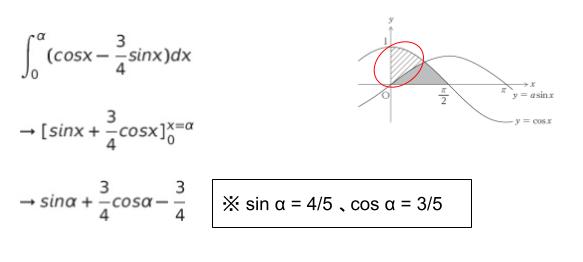
斜線部の面積は、α を用いて定積分で表すと
∫ (上端の式ー下端の式) dx　x：0 → α なので

以下のように計算すると
4/5 + 3/4 × 3/5 – 3/4
= (16 + 9 – 15)/20
= 1/2 となり、ちょうど面積を 2 等分することがわかります。

以上より、正解は 3 です。