問 題
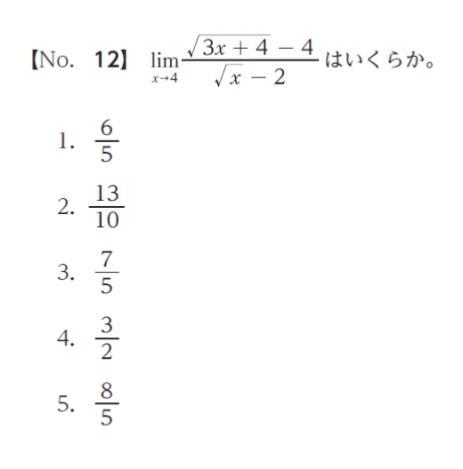
正解.4
解 説
【解法 1:ロピタルの定理】
分母・分子をそれぞれ微分した後で、値を代入してもよいというのがロピタルの定理です。0/0 型や ∞/∞ 型の時に有効な手段です。
分母:√x = x1/2 なので、微分すると (1/2) × 1/√x …(1) です。 (1) に x = 4 を代入すれば 1/4 です。※ x-1/2 = 1/√x です。
分子:√3x + 4 = (3x + 4)1/2 なので、微分すると (3/2) × 1/√(3x + 4) …(2) です。(2) に x = 4 を代入すれば 3/8 です。
求めたい極限は、ロピタルの定理より
(3/8)/(1/4) = 3/2 です。
以上より、正解は 4 です。
【解法 2 0/0 型なので、約分】
x – 4 = X とおきます。x = X + 4、lim X → 0 となります。以下のような式変形により、分母・分子に 0 が残らないようにして、極限を求めます。
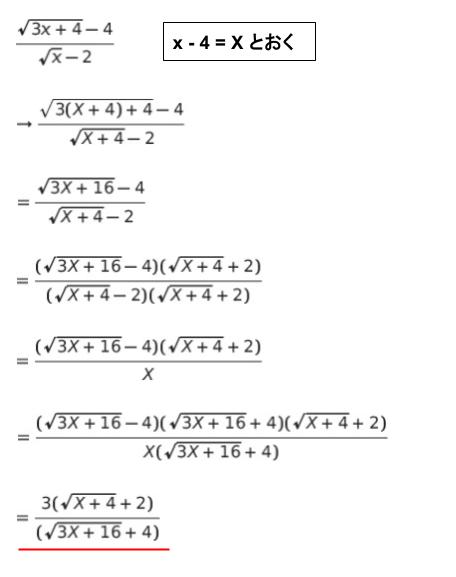
以上より、正解は 4 です。

コメント