問 題
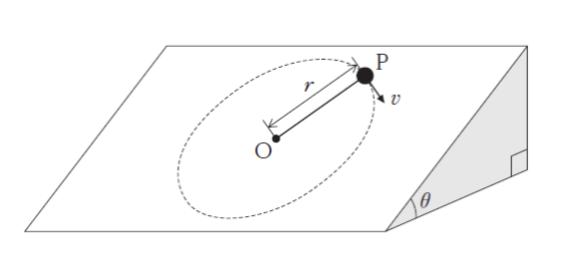
図のように、水平面と角 θ ( 0 < θ < π/2 ) をなす滑らかな斜面があり、小球 P が一端についた長さ r の糸の他端を斜面上の点 O に取り付けた。斜面上で P に円運動をさせたとき、糸がたるまないための最高点における P の速さ v の最小値として最も妥当なのはどれか。ただし、重力加速度の大きさを g とする。
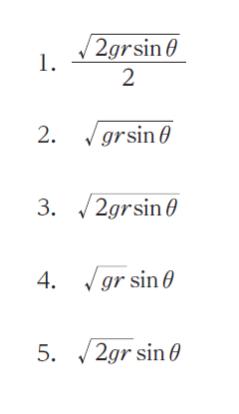
正解.2
解 説
・斜面上の小球 P として注目すれば
中心方向への力が mg sinθ…(1) です。
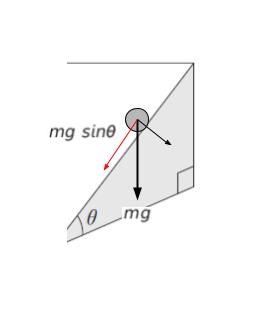
・最高点における 速さを vP とおくと
遠心力の公式から F = mvP2/r…(2) です。
(2) ≧ (1) が、糸がたるまない条件と考えられます。解けば vP ≧ √grsinθ です。従って、v の最小値は √grsinθ です。
以上より、正解は 2 です。

コメント