問 題
アリルラジカル (•CH2-CH=CH2) の三つの π 電子について、ヒュッケル近似を用いたところ、電子のエネルギーを E、クーロン積分を α、共鳴積分を β として、次の永年方程式を得た。
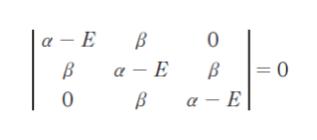
アリルラジカルの最も安定な電子配置における π 電子系の全エネルギーとして最も妥当なのはどれか。
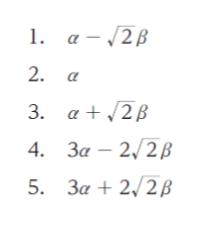
正解.5
解 説
まず永年方程式を解きます。3 行 3 列の行列式なので、サラスの公式です。0 が多くて結構計算が楽なのは嬉しいところです。
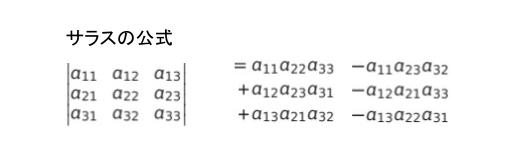
(α – E)3 – 2β2(α – E) = 0 なので
(α – E){(α – E)2 – 2β2} = 0 として
E = α、α ± √2β を得ます。
量子力学特有の考え方ですが 同符号の α + √2β が 結合性軌道でエネルギー的に最も低く安定な軌道と対応します。この軌道に電子が 2 つ入ります。残り 1 つの電子が次に安定な α の軌道に入ります。
従って、全エネルギーは
2 × (α + √2β) + α = 3α + 2√2 β です。
以上より、正解は 5 です。

コメント