問 題
物質 A から中間体 B を経由して C が生成する反応、A → B → C がある。この素反応はいずれの段階も 1 次反応であり、 1 段階目の反応の速度定数 k1 は 7.39 × 10-2 s-1、 2 段階目の反応の速度定数 k2 は 1.00 × 10-2 s-1 である。
反応開始時の A、B、C の濃度 [A]0、[B]0、[C]0 をそれぞれ、[A]0 = 2.00 × 10-2 mol・L-1、[B]0 = [C]0 = 0 mol・L-1 としたとき、この反応に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。
ただし、loge 7.39 = 2.00、loge 2 =0.690、loge 10 =2.30 とする。
「この逐次反応の各物質の分解及び生成速度は、
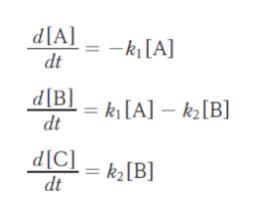
であり、この微分方程式を解くと、A の濃度は、[A] = [A]0e-k1t となる。また、B の濃度は[B] = ㋐となる。
反応開始時からB の濃度が最大となるまでの時間は、d[B]/dt = 0 となる時間であることから、㋑ となる。」
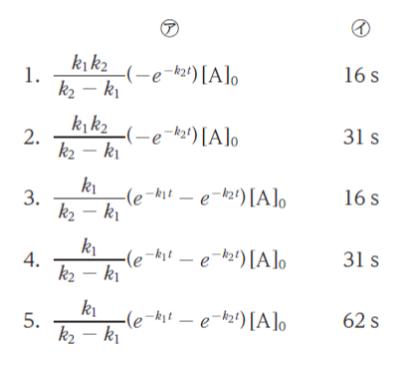
解 説
【㋐ について】
d[B]/dt = k1[A] – k2[B] に、問題文から解かれている [A] = [A]0 e-k1t を代入します。
d[B]/dt = k1 [A]0 e-k1t – k2[B]
d[B]/dt + k2[B] = k1 [A]0 e-k1t と変形すれば
y’ + P(x)y = Q(x) 型 の 1 階線形微分方程式 です。一般解の公式は覚えている設定と思われます。ただ、公式を覚えていてもなお、この場で解くのは時間的に厳しいと思われます。
そこで、選択肢の活用がおすすめです。
k1 がとてつもなく大きいとします。すると A → B が一瞬で進行するので、ほぼ B → C とみなせます。また [A] :[A]0 → 瞬時に 0、[B] :0 → 瞬時に [A]0 となります。
A → B だけであれば [A] = [A]0 e-k1t なので
B → C だけであれば [B] = [B]0 e-k2t です。※ 初濃度は [B]0 = [A]0 です。
初濃度を書き換えれば [B] = [A]0 e-k2t …(1) です。
選択肢 1,2 ですが
k1 >> k2 なら 分母を -k1 と近似できます。すると k2(e-k2t) [A]0 です。(1) と比較すると、係数 k2 が残るため、誤りです。正解は 3 ~ 5 です。
ちなみに、選択肢 3 ~ 5 の式では
k1 >> k2 なら 分母は -k1 と近似できます。また、( ) の中身部分は e-k1t << e-k2t なので -e-k2t と近似できます。するとうまく (1) と同じ形です。
【㋑ について】
d[B]/dt を計算します。定数部分は無視してよいので
f(t) = e-k1t – e-k2t とおきます。
f'(t) = -k1e-k1t + k2e-k2t …(2) です。
(2) = 0 の時
k1e-k1t = k2e-k2t です。少し変形して
k1/k2 = e(k1t – k2t) 辺々 自然対数をとって
ln(k1/k2) = (k1 – k2)t となります。
t について解けば
t = ln(k1/k2)/(k1 – k2) です。
k1/k2
= (7.39 × 10-2)/(1.00 × 10-2)
= 7.39
→ ln(k1/k2) = ln7.39 は、問題文ただし書きより 2.00 です。
k1 – k2
= 0.0739 – 0.01
= 0.0639 です。
従って
t = 2.00/0.0639 ≒ 31 となります。㋑ は「31s」です。
以上より、正解は 4 です。

コメント