問 題
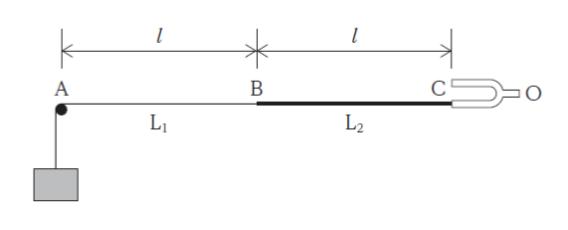
図のように、線密度がそれぞれ ρ、4ρ の糸 L1、L2 の一端どうしを点 B でつなぎ、L2の他端 C に水平にした振動数 f の音叉 (おんさ) O の先端をつなぎ、L1 の他端には滑車 A を介して小物体をつるした。AB 間、BC 間の糸は水平で、その長さは共に l で等しい。
いま、O を振動させたところ、AB 間、BC 間の糸は共振し、AB 間には、A、B を節として2 個の腹をもつ定常波ができた。このとき、BC 間にできる定常波において、腹の位置の糸の振動数と腹の個数の組合せとして最も妥当なのはどれか。
ただし、滑車の大きさは無視できるものとし、糸の線密度と張力の大きさをそれぞれt、S とすると、糸を伝わる波の速さ v は次式で与えられるものとする。

正解.3
解 説
AB 間における「A、B を節として2 個の腹をもつ定常波」とは、以下のような定常波です。
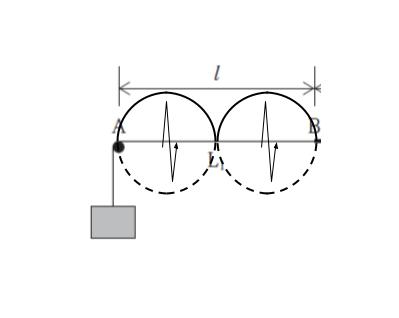
BC 間にできる定常波について、音叉とつながっているので AB 間も BC 間も 振動数は変化しません。振動数は f です。正解は 3 or 4 です。
問題文で与えられた v = √S/ρ より、張力が一定であれば、波の速さは「線密度 の平方根に反比例」です。
BC 間の 糸を伝わる波の速さ v2 は、線密度 L2 が L1 の 4 倍なので、L1 における波の速さを v1 とすれば、v1 の 1/2 倍であるとわかります。v2 = v1/2 です。
波の基本式 v = fλ より
f が一定で v が半分であれば、波長 λ が半分であるとわかります。波長 が半分の定常波を描けば、以下のようになります。従って、腹の個数は「4 個」です。
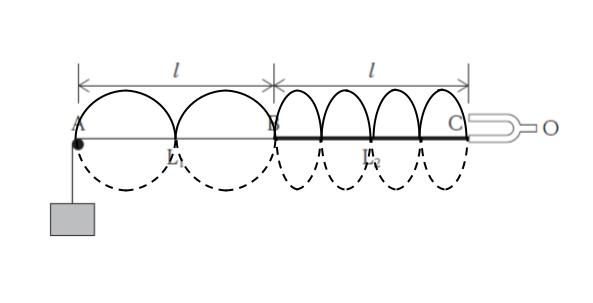
以上より、正解は 3 です。

コメント