問 題
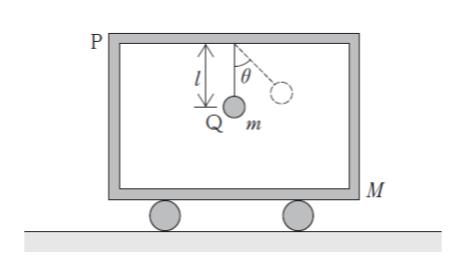
滑らかで水平な地面に静止した質量 M の台車 P において、図のように、P の天井から質量m の小球 Q を長さ l の糸によってつり下げた。糸がたるまないようにしながら、糸が鉛直方向と角 θ ( 0 < θ < π/2 ) をなす位置まで Q を持ち上げ、全体が静止した状態で Q を静かに放した場合、最下点に達したときの地面に対する Q の速さとして最も妥当なのはどれか。ただし、重力加速度の大きさを g とする。
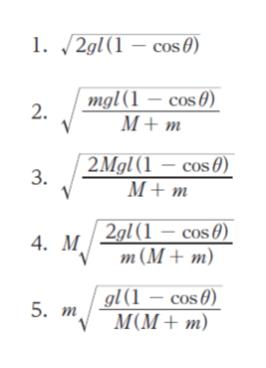
解 説
解法 1【選択肢の活用】
M がとてつもなく大きくてほぼ動かないとします。すると最下点に達した時の小球 Q の速さは、最下点を基準とした位置エネルギー U = mg{l(1 – cos θ)}…(1) が、運動エネルギーに変換されて mv2/2…(2) になるので、mg{l(1 – cos θ)} = mv2/2 を解けば √2gl(1 – cosθ) です。
M が小さい時は 台車が動いて地面に対する速さが変わるはずなので、M が含まれない選択肢 1 は誤りです。
M が大きい時に
選択肢 2 → 0
選択肢 4 → ∞
選択肢 5 → 0 です。
√2gl(1 – cosθ) に近づくのは選択肢 3 のみです。
以上より、正解は 3 です。
解法 2 【運動量、力学的エネルギー 保存則】
最下点での Q の速さを v、そのときの P の速さを V とおきます。
・運動量保存 (水平方向) より
mv + MV = 0…(1)
・力学的エネルギー保存により
mv²/2 + MV²/2 = mg{l(1 – cos θ)}…(2)
(1) から V = mv/M より V を消去して
v について解くと
v = √2Mgl(1 – cosθ)/(M + m) を得ます。
以上より、正解は 3 です。

コメント