問 題
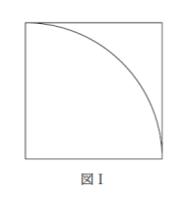
図Ⅰのような 1 辺の長さ 1 の正方形と半径 1 で中心角 90° の扇形を考える。
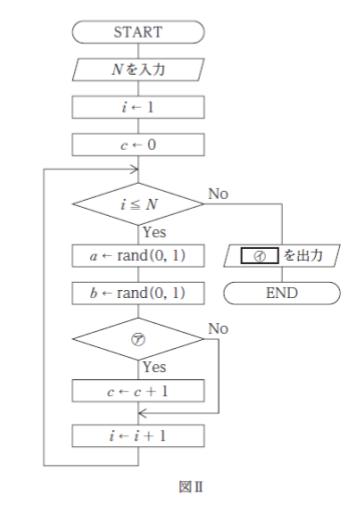
図Ⅱは、図Ⅰの正方形内にランダムに N 個の点を散布した際に、N 個に対する扇形内の点の個数の比を用いて、円周率 r の近似値を出力するフローチャートである。図Ⅱ中の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのは次のうちではどれか。
ただし、N を十分大きな正の整数とする。また、rand (0、1) は、 0 以上 1 未満の実数の一様乱数を生成する操作を表す。
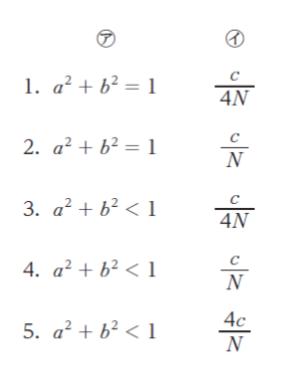
正解.5
解 説
㋐ ですが
a2 + b2 = 1 では、例えば a = 1,b = 0 のように、ピンポイントに円周と対応した値が出なければ yes になりません。すると、c はほとんど増えず、最終的に ほぼ 0 が出力されるチャートとなってしまいます。㋐ は a2 + b2 < 1 が妥当です。正解は 3 ~ 5 です。
㋑ ですが
正方形の面積が 1 で、円の内側の面積が π/4 (大体 0.78) なので、c は 確率 大体 0.78 で yes となり、カウントされていきます。N 回チャートが回り終わった時に、c は大体 0.78 N になるということです。すると、c/N を出力すると、それは「π/4」の近似値です。
出力したいのは「π の近似値」なので c/N の 4 倍が妥当です。㋑ は 4c/N です。
以上より、正解は 5 です。

コメント