問 題
軽いばねの一端を天井に固定し、ばねの他端に小物体を取り付けた。ばねが自然長でかつ鉛直になるよう、小物体を板で下から支え、この状態を初期状態とした。
初期状態から、板を鉛直方向にゆっくりと下げていったとき、ばねの自然長からの伸びの最大値は x1 となった。また、初期状態に戻してから、板を瞬間的に取り除いたとき、ばねの自然長からの伸びの最大値は x2 となった。このとき、 x2/x1 はおよそいくらか。
解 説
小物体の質量を m、ばね定数を k とします。
【初期状態からゆっくり下げていった x1】
ゆっくりと小物体の重さでばねが伸びていき、ばねが x1 伸びたところで止まります。板を外しても止まっているイメージができるのではないでしょうか。
ばねが出てきたら、フックの法則を思い出します。F = kx1 です。質量 m なので、下向き mg の力が作用します。そのため、mg = kx1 ∴ x1 = mg/k です。
【初期状態から板を瞬間的に取り除いた x2】
小物体は単振動します。どの時点でも力学的エネルギー保存則が成り立ちます。位置エネルギーの基準を自然長の高さとします。
1:自然長の時の力学的エネルギー
位置エネルギー 0、運動エネルギーは静止しているので 0、ばねが自然長なので、弾性力による位置エネルギーも 0 です。和は 0 です。
2:x2 伸びた所の力学的エネルギー
位置エネルギーは -mgx2、運動エネルギー 0、弾性力による位置エネルギー kx22/2 です。和は「-mgx2 + kx22/2」…(1) です。
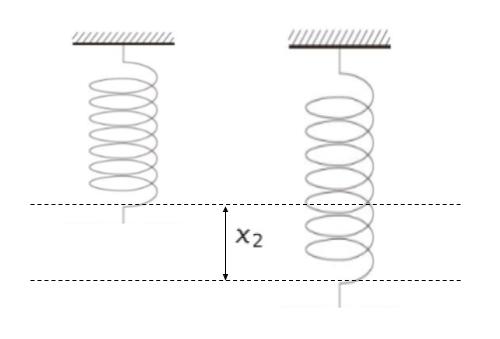
力学的エネルギーの和が変わらないので、(1) = 0 です。x2 について解けば、x2 = 2mg/k です。
従って
x2/x1
= (2mg/k)/(mg/k)
= 2 です。
以上より、正解は 4 です。

コメント