国家公務員総合職（化学・生物・薬学）R4年 問1解説

　問 題　　　　　

赤玉 3 個と白玉 3 個が入った袋がある。この袋に対し、次のⅰ、ⅱからなる一連の操作を 2 回行ったとき、袋の中の赤玉の個数が 3 個となる確率はいくらか。

 

 

 

 

 

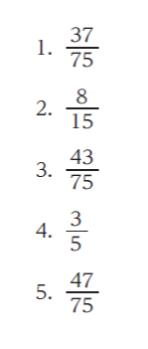
　解 説　　　　　

確率の定義は「該当する通り/全ての通り」です。

・1 回操作を行って、色違いの玉を取り出す確率について考えます。1 回の操作における全ての通りは、6 個の玉から 2 個玉を取り出す通りなので、₆C₂ = 15 通り です。

色違いの玉を取り出す通りは、赤 3 個から 1 個取り出し、白 3 個から 1 個取り出す通りなので、₃C₂ × ₃C₂ = 9 通りです。従って、「1 回操作を行って、色違いの玉を取り出す確率」は 9/15 = 3/5 です。

・1 回操作を行って、同じ色を取り出す確率について考えます。 「色違いの玉を取り出さない確率」といえるので、「1 – 3/5 = 2/5」です。

 

【パターン１：1 回目　色違いの玉】
1 回目に　色違いの玉を取り出した場合、袋の中の玉は 赤 3 個、白 3 個で変わりません。すると、2 回目の操作でも色違いの玉を取り出せば、袋の中の赤玉の個数は 3 個です。この確率は 3/5 × 3/5 = 9/25 と表すことが出来ます。

【パターン２：1 回目　色が同じ玉】
1 回目に　同じ色の玉を取り出した場合、袋の中の玉は どちらかの色の玉が 5 個、もう片方の色の玉が 1 個になります。すると、2 回目の操作でたくさんある方の色の玉を 2 個取った場合にのみ、元に戻って赤が 3 個になります。2 回目の操作でたくさんある方の色を 2 個取る確率は ₅C₂/₆C₂ = 10/15 = 2/3 です。従って、このパターンの確率は 2/5 × 2/3 = 4/15 となります。

求める確率は、パターン 1 ＋ パターン 2 です。
9/25 + 4/15
= (27+20)/75
= 47/75 です。

以上より、正解は 5 です。