問 題
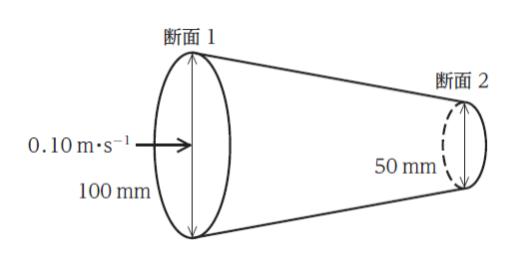
図のように、滑らかに変化する断面をもつ円管があり、その中を 20 ℃ の水が管を満たした状態で定常的に流れている。
断面 1 の直径が 100 mm、断面 2 の直径が 50 mm、断面 1 における平均流速が 0.10 m・s-1 であったとき、断面 2 における平均流速と管内流れの組合せとして最も妥当なのはどれか。ただし、20 ℃ における水の密度は 1000 kg・m-3、粘度は 1.0 × 10-3 Pa・s とする。
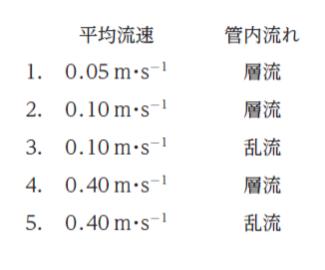
正解.5
解 説
平均流速について、連続の式を思い出します。断面 1 と 断面 2 において、Q = A1v1 = A2v2 が成立します。直径が断面 1 → 断面 2 で半分になっているので、断面積は 1/4 になります。このため、流速は 4 倍になります。
断面 1 における平均流速が 0.10 なので、断面 2 における平均流速は、0.10 × 4 = 0.40 m・s-1 です。正解は 4 or 5 です。
管内流れが層流か乱流かの判断は、レイノルズ数 (Re) で行います。
Re = Vd/ν です。V は流速、d は代表長さ と呼ばれ、円管であれば直径がよく用いられます。ν は動粘度です。ν = μ/ρ です。粘度を密度で割ったものが動粘度です。
本問断面 2 におけるレイノルズ数は
Re = (0.40 × 50 × 10-3)/(1.0 × 10-3/1000)
= 20 × 103 > 4000 より、乱流と考えられます。
以上より、正解は 5 です。

コメント