問 題
ドップラー効果に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。
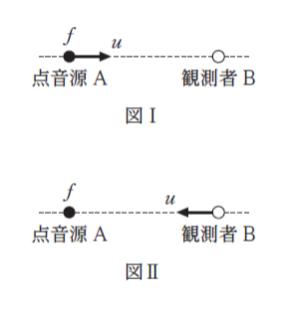
「図Ⅰのように、静止している観測者 B に向かって、振動数 f の音を出す点音源 A が一定の速さ u で移動しているとき、B が観測する音の波長 λ1 は ㋐ であり、その振動数を f1 とする。
また、図Ⅱのように、振動数 f の音を出す点音源 A が静止しており、A に向かって、観測者B が一定の速さ u で移動しているとき、B が観測する音の振動数を f2 とすると、f1 と f2 の大小関係は、㋑ となる。ただし、音速を V とし、V > u > 0 とする。」
解 説
ドップラー効果の具体例は、消防車を 止まって聞いてると音が高く聞こえるといったものです。音源が 近づいてくる → 高くなる = 振動数 大きくなってる。という関係があります。
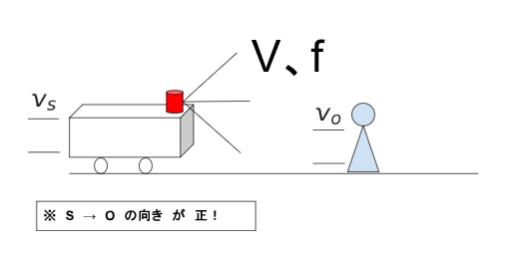
ドップラー効果では、まず「音源と観測者が同じ方向に移動している図」を考えるとよいです。以下のイメージです。小文字 s は source の略、音源を表します。小文字 o は observer の略、観測者を意味します。
ドップラー効果の公式が以下です。

これをふまえると、図Ⅰは vs = u、vo = 0 です。
f’ = V/(V – u) × f…(1) です。
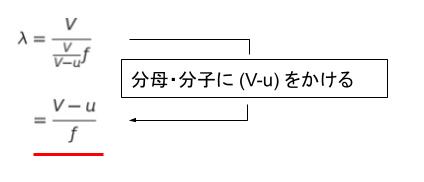
波長 λ についてですが、V = fλ なので、λ = V/f…(2) です。(2) の f の所に (1) の右辺を代入すれば、(V-u)/f となります。正解は 4 or 5 です。計算過程は以下の通りです。
② ですが
図Ⅱでは、vs = 0、vo = -u となります。f2 = (V+u)/V × f です。
f1 と f2 の大小関係は、具体的な数で考えるとわかりやすいです。例えば、V = 100、u = 1 とすれば f1 = 100/99 、f2 = 101/100 です。f1 の方が大きくなります。f1 > f2 です。
以上より、正解は 5 です。

コメント