国家公務員総合職（化学・生物・薬学）R3年 問14解説

　問 題　　　　　

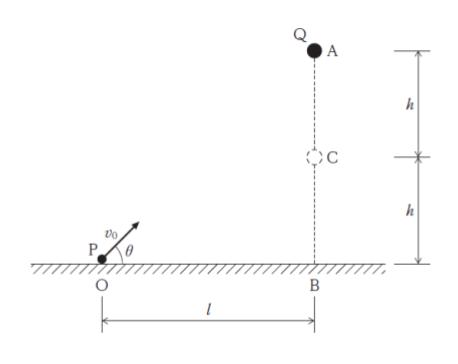
図のように、水平な地表面より高さ 2h の点 A から小球 Q を初速 0 で自由落下させると同時に、A の真下にある地表面上の点 B より l 離れた地表面上の点 O から小球 P を速さ v₀、地表面からの角度 θ (0 < θ < π/2) で発射した。

Q が B より高さ h の点 C に到達する前までの間に、P と Q が衝突するために必要な v₀ の条件として最も妥当なのはどれか。ただし、P、Q の運動は O、A、B を通る平面内で起こるものとし、重力加速度の大きさを g とする。

 

 

 

 

 

　解 説　　　　　

いわゆるモンキーハンティングの問題です。初見の場合、まず無理です。一般的に解ける人でも、試験合格のためには解けなくてもよくて、時間を使いすぎないことが重要です。

v₀ がとてつもなく速い場合を考えます。小球 Q が落ちる間もなく、小球 P が水平方向に l 進むのだとすると、初めにぴったり Q を狙っていないと当たりません。つまり ベクトル v₀ の延長方向に Q があります。ここで直角三角形 OAB を考えると l × tan θ = 2h です。tanθ = 2h/l と表すことができます。

具体的に考えます。θ = 45° (π/4) とすれば、tan 45° = 1 だし、l = 2h となって 変数も 1 個減って都合が良さそうです。

【θ = 45°、小球 P の 水平方向変位】
小球 P 水平方向の初速は v₀/√2 です。
水平方向に力は作用しないので等速運動です。
時刻 t における変位は、x = (v₀/√2) × t …(1) です。

小球 P が Q と当たる時、x はちょうど l です。(1) の左辺を l とすれば、t について解くと t = √2 l/v₀ …(3) です。

【θ = 45°、小球 P の垂直方向の変位】
t = 0 の時を 位置 0 として、地面に向かう方向を正とします。

自由落下なので Qy = gt²/2…(2) です。点 C に到達する時 Q_y = l/2 なので、(2) の左辺を l/2 とすれば、t について解くと t = √(l/g) …(4) です。

(3) の時間が、小球 Q が 点 C に到達してしまう時間である (4) よりは小さくないと、小球 Q が点 C を通過してしまいます。つまり「√2 l/v₀ < √(l/g)」が必要な条件です。v₀ について解けば、v₀ > √(2g/l) とわかります。

θ = 45°、2h = l、4h² = l² の時、l を消去すれば
選択肢 1 は　v₀ > √(5/4) × (g/l) なので誤りです。

選択肢 2 は　v₀ > √(5/8) × (g/l) なので誤りです。

選択肢 3 は　v₀ > √(g/l) なので誤りです。

選択肢 4 は　v₀ > √(5/4) × (g/l) なので誤りです。

選択肢 1 ~ 4 誤りです。

以上より、正解は 5 です。