問 題
袋の中に 1 から 7 までの数字が一つずつ書かれた 7 個の球が入っている。この袋の中から無作為に1 個の球を取り出し、球に書かれた数字を記録してから袋の中に戻す試行を 2 回繰り返す。
1 回目及び 2 回目に出た球の数字をそれぞれ A、B とするとき、確率変数 10A + B の標準偏差はいくらか。なお、確率変数 X の分散を V(X)と表すとき、任意の定数 a に対し V(aX)=a2V(X)が成り立つ。
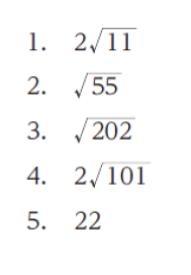
正解.4
解 説
標準偏差は、√分散 です。
分散は 「変数 X の 2 乗 の平均」ー「変数 X の平均 の 2 乗」で求めることができます。
変数 X として、1,2,3,4,5,6,7 を取るので
変数 X2 は 1,4,9,16,25,36,49 です。それぞれの確率は 1/7 なので、平均は
(1+4+9+16+25+36+49)/7 = 20 です。
変数 X の平均は 1~7 の真ん中なので 4 です。
変数 X の平均の 2 乗は 16 です。
V(A) = V(B)
= 20 – 16 = 4 です。
V(10A + B)
= 100V(A) + V(B)
= 100 × 4 + 4
= 101 × 4
√ V(10A + B)
=√(101 × 4)
= 2 √101 となります。
以上より、正解は 4 です。

コメント