問 題

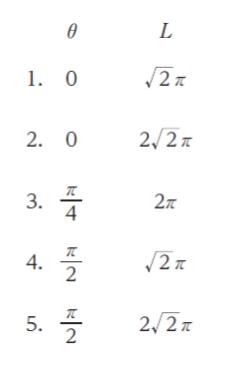
正解.4
解 説
具体的に考えるのがおすすめです。
t = 0 の時、点 P は (2,0,0) です。
t = π/2 の時、点 P は (1,1,√2) です。
t = π の時、点 P は (0,2,0) です。
できるだけ正確に、手元に図を書きます。t = 0,π/2,π の時の 3 点を滑らかに結び、動点 P の概略を描きます。
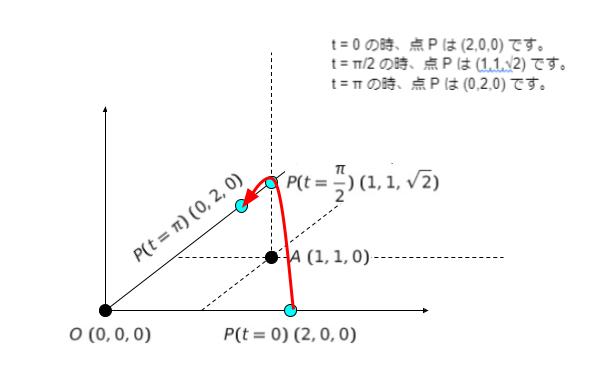
OA と AP のなす角を θ とした時に、選択肢から 0 か π/4 か π/2 であるということなので、P(t = π/2) の時の OA と AP のなす角に注目すれば、明らかに直角であることが読み取れるのではないでしょうか。θ は「π/2」です。正解は 4 or 5 です。
曲線の長さは、選択肢より √2 π か 2 √2 π かです。曲線を直線で近似すれば、(2,0,0) と (1,1, √2) の距離は 2 です。(1,1, √2) と (0,2,0) の距離も 2 です。合わせて 4 なので、4 に近い方を選べば √2 π です(一例として、√2 ≒ 1.4、π ≒ 3.1 で評価すればよいです)。
以上より、正解は 4 です。

コメント