問 題
次の記述の ㋐、㋑ に当てはまるものの組合せとして正しいのはどれか。
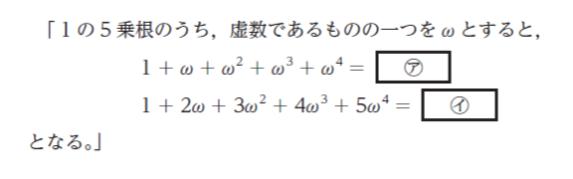
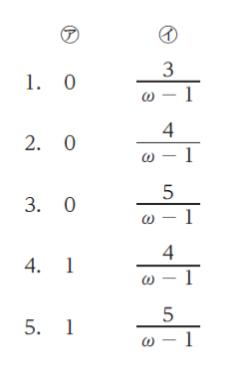
正解.3
解 説
1 の 5 乗根は「x5 = 1」…(1) の解です。
x = 1 が解の 1 つですが、虚数ではありません。
x = 1 が解の 1 つであることから、(1) を変形して
x5 – 1 = 0 とすれば、左辺は (x – 1)(…) = 0 と変形できます。
左辺を x – 1 で割れば
(x – 1)(x4 + x3 + x2 + x + 1) = 0 です。x ≠ 1 であれば、その解を ω とすると
ω4 + ω3 + ω2 + ω + 1 = 0 となります。㋐ は 0 です。
1 + 2ω + 3ω2 + 4ω3 + 5ω4 という式は、数字だけ見れば 1,2,3… と「1 ずつ増えて」います。等差数列です。文字部分は、初めを ω0 が掛けられているとすれば ω0、ω1、ω2…と「ω をかけた分ずつ増えて」います。等比数列です。
『等差 × 等比 型の数列』では
1:まず和を S とおく
2:等比数列の公比 r をかけた rS を考える
3:S – rS に注目する という流れが定石です。
本問では
S = 1 + 2ω + 3ω2 + 4ω3 + 5ω4
ωS = ω + 2ω2 + 3ω3 + 4 ω4 + 5 ※ ω5 = 1 に直しています。
S – ωS = 1 + ω + ω2 + ω3 + ω4 – 5
(1 – ω)S = -5
∴ S = 5/(ω – 1) となります。㋑ は 5/(ω – 1) です。
以上より、正解は 3 です。

コメント