問 題
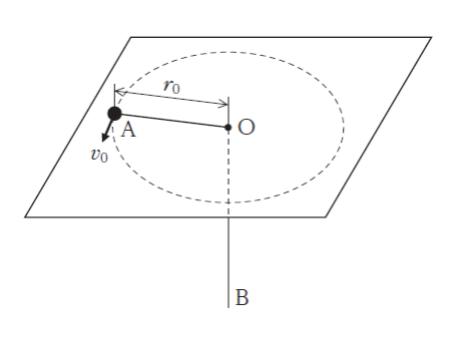
図のように、水平に固定した滑らかな板の中心 O に小さな穴を開けて糸を通し、糸の一端 A に小球を付け、糸の他端 B を手で持ち、半径 r0、速さ v0 で小球を等速円運動させた。この状態から、B をゆっくり引いて、半径を r0 から r1 (r1 < r0) にして小球を等速円運動させたとき、小球の速さとして最も妥当なのはどれか。
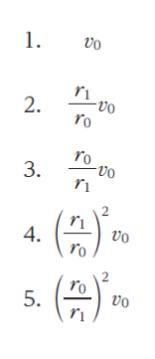
解 説
半径が変わる円運動の問題です。初見だったり、解き方を知らない場合は、具体的にイメージして 2 択までしぼりたい問題です。
ひもの先に鉄球をつけて (モーニングスター をイメージするとよいです) ある程度の長さでブンブン回すイメージをしてみます。「甘寧一番乗り」を知っていれば、その絵の雰囲気で、ヘリコプターのように床と水平に鉄球を振り回すイメージです。
この時、振り回すひも部分が長いとゆっくり回って、ひも部分が短いと ぎゅんぎゅん速く回るように想像できるのではないでしょうか。つまり r0 → r1 になると、v は大きくなると考えられます。そのため、速度が変化しない 選択肢 1、及び 速度が小さくなる 選択肢 2,4 は誤りです。正解は 3 or 5 です。
解き方は面積速度一定の法則を使います。「作用する力が中心力のみの場合、角運動量が保存されます」。これを言い換えたものが「面積速度一定の法則」です。面積速度は 時間あたりに移動する面積と考えればよいです。
等速円運動において、面積速度一定の法則より
それぞれの半径における速度を v0、v1 とおけば
「r0 における面積速度 r0v0/2」 と
「r1 における面積速度 r1v1/2」 が等しくなります。
つまり
r0v0/2 = r1v1/2 です。v1 = … の形にすれば
v1 = (r0/r1) × v0 です。
以上より、正解は 3 です。

コメント