問 題
a = 1 – 3√5 のとき,a4 – 2 a3 + 9 a + 7 はいくらか。
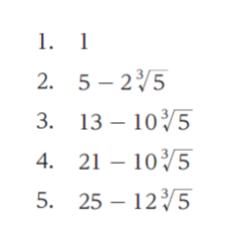
解 説
【解法 1:選択肢の活用、具体的に考えて評価 現実的でおすすめ】
3√5 とは「3 乗したら 5 になる数」です。
1.63 = 4.096 ≒ 4.1
1.73 = 4.913 ≒ 4.9 なので、3√5 は、大体 1.7 とします。
すると選択肢は
1. 1
2. 5 – 2 × 1.7 = 1.6
3. 13 – 10 × 1.7 = -4
4. 21 – 10 × 1.7 = 4
5. 25 – 12 × 1.7 = 4.6 と評価できます。
a = 1 – 1.7 = -0.7 とします。
a2 = (-0.7)2 = 0.49 ≒ 0.5 です。(a2)2 = a4 = 0.25
a3 = 0.5 × -0.7 = -0.35 となります。
これで 与えられた式は
a4 – 2 a3 + 9 a + 7
→ 0.25 -2 × (-0.35) + 9 × (-0.7) + 7
= 1.65 です。大体ですが 1.5 ~ 2 ぐらいと評価できました。
従って
選択肢から選べば 5 – 2 × 3√5 が妥当です。
以上より、正解は 2 です。
【解法2:式の変形で字数下げ】
a = 1 – 3√5 より a -1 = – 3√5
両辺を 3 乗して a3 -3a2 + 3a -1 = -5
∴ a3 -3a2 + 3a +4 = 0
(a4 – 2 a3 + 9 a + 7) ÷ (a3 -3a2 + 3a +4) を計算すると
商が a + 1、余りが 2a + 3
A ÷ B = Q…R の時、A = BQ + R なので
a4 – 2 a3 + 9 a + 7 = 0 × (a+1) + 2a + 3
右辺は計算すれば 2a + 3 となる。
結局、2a + 3 を求めればよい。
a = 1 – 3√5 を代入すれば
2 (1 – 3√5) + 3
= 5 – 23√5
以上より、正解は 2 です。

コメント