国家公務員総合職（化学・生物・薬学）R2年 問40解説

　問 題　　　　　

A から B が生成する反応は、次の反応式で表され、A についての一次反応である。

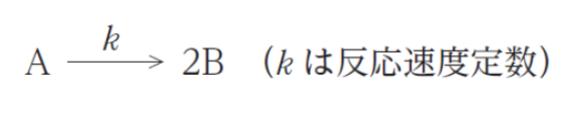
この反応を等温回分反応器を用いて、次の条件で行い、B を 1 時間当たり 3.0 × 10⁴ mol 生成したい。

このとき、必要な反応器の体積はおよそいくらか。ただし、log_e 0.2 = -1.6 とする。

1． 1.4 m³
2． 2.8 m³
3． 3.1 m³
4． 5.6 m³
5． 6.2 m³

 

 

 

 

 

　解 説　　　　　

一次反応なので、半減期 T_1/2 = ln2/k です。※ ln2 ≒ 0.7 も含め、基礎知識です。問われているのが 1 時間あたりなので、3600 をかけて k の単位を時間あたりに直すと、 k = 1.0 × 10^-4 /s → 0.36 /h です。半減期は 0.7/0.36 ≒ 2 時間とわかります。

反応器の体積が仮に 1m³ とすると、条件より A の濃度が 3.0 × 10⁴ なので、A が 3.0 × 10⁴ mol 存在します。

反応率 80% にいたるのは、大体 「2 半減期」過ぎたころです。つまり大体 4 時間後です。前処理と後処理の 30 分 × 2 を考慮すれば「計 5 時間」反応にかかります。

できあがる B の量は 反応式から「A の 80% × 2」です。5 時間かけて 4.8 × 10⁴ mol 生成なので、1 時間あたり ほぼ 1 × 10⁴ mol 生成です。

1 時間あたり B を「3 × 10⁴」mol ほしいので、必要な体積は 3 倍です。最も近い値を選択肢から選べば 3.1 m³ です。

以上より、正解は 3 です。

ちなみに、log_e0.2 = -1.6 は
[A] = [0.2A] になる時の時間 t を正確に求める場合に用います。

一次反応なので
[A] = [A₀]e^-kt です。ここで [A] = [0.2A] を代入し、両辺 ln 取った時に用いるヒントです。

参考　微分型速度式の積分型速度式への変換
https://yaku-tik.com/yakugaku/bk-4-1-2/