問 題
直径 D1 の 2 本の円管が合流して直径 D2 (= 2D1) の円管となる流路がある。直径 D1 の円管を流れる流体は同じ平均速度で滑らかに合流する。直径 D1 の円管を流れる流体のレイノルズ数 Re1 と直径 D2 の円管を流れる流体のレイノルズ数 Re2 の比 Re1/Re2 はおよそいくらか。
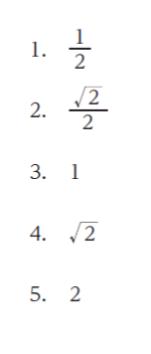
正解.3
解 説
円管のレイノルズ数は Re = ud/ν …(1) です。
u が平均流速、d が内径、ν が動粘度です。これは基礎知識です。
円管が合流すると、直径が 2 倍になっているかわりに、流量が2倍、断面積が 4倍だから連続の式 Q = Av より、v は 1/2 倍になります。
従って
(1) の u が半分、d が 2 倍になるので、レイノルズ数は不変です。Re1 = Re2 です。比は 1 です。
以上より、正解は 3 です。
類題 H27 no39 レイノルズ数
https://yaku-tik.com/yakugaku/km-27-39/

コメント