問 題
主曲率半径 r1、r2 により定義される曲面をもつ界面内外の圧力差 ΔP は、界面張力を γ として、次の Young ‒ Laplace の式で表される。
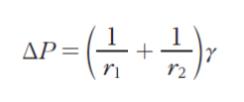
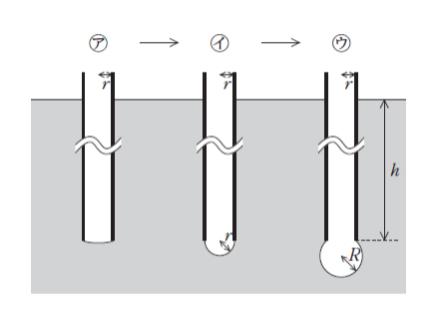
図のように、液体中に深く挿入した半径 r の円形断面をもつ毛細管に気体を吹き込んで気泡を形成させることを考える。気泡半径を R としたとき、図中の ㋐、㋑、㋒ のそれぞれの段階において気泡成長時間と気泡内圧力との関係を定性的に表したものとして最も妥当なのはどれか。
ただし、気泡表面は球面とし、液面から毛細管先端までの距離 h は、r、R と比べ、十分に大きいものとする。また、気体の密度は、液体の密度と比べ無視できるものとする。
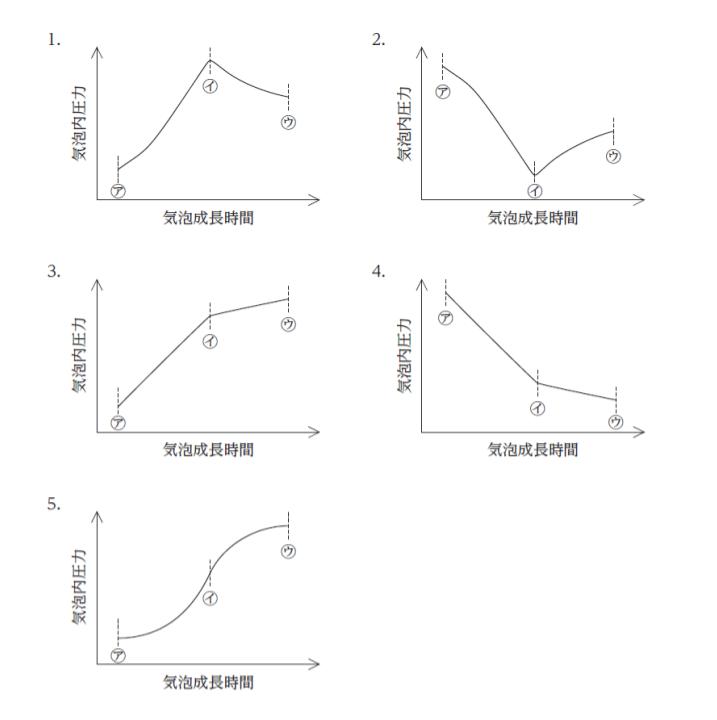
正解.1
解 説
曲率半径のイメージは
曲線を強引に円弧の一部としてみた時の円の半径です。
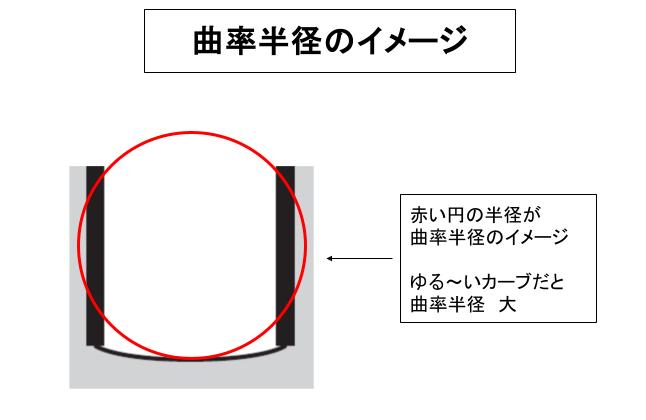
主曲率半径 r1、r2 は ㋑ 以前では 符号が 正、㋑ 以降では 符号が負となります。符号は知識として見たことがないとピンとこないと思われます。
そのため
気泡内圧力は 問題文の Young – Laplace の式より ㋑ > ㋒ とわかります。選択肢 2,3,5 は誤りです。
また、㋐ と ㋑ について
主曲率半径 r1,r2 が ㋐ の方が大きくなります。そのため、ΔP が小さくなります。従って、気泡内圧力は ㋐ < ㋑ です。選択肢 4 は誤りです。
以上より、正解は 1 です。

コメント