問 題
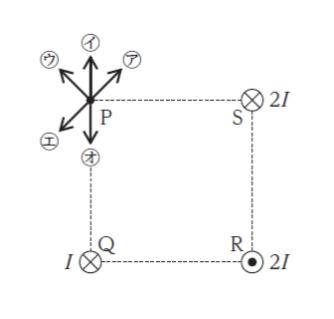
図のように、正方形 PQRS の三つの頂点 Q、R、S に、 3 本の十分に長い直線導線を正方形に対して垂直に配置し、Q、S を通る導線に、紙面の表から裏の向きにそれぞれ大きさ I 、2I の電流を、R を通る導線に、紙面の裏から表の向きに大きさ 2I の電流を流した。
このとき、図中の矢印 ㋐ ~ ㋔ のうち、 3 本の導線に流れる電流によって P に生じる磁界の向きを表すものとして最も妥当なのはどれか。
1.㋐
2.㋑
3.㋒
4.㋓
5.㋔
正解.2
解 説
直線電流が作る磁界と来たら「アンペールの法則」です。距離 r 離れたら H = I/2πr です。ちなみに、本問では使いませんが、円電流が出てきて、中心の磁界と来たら「ビオ・サバールの法則」です。H = I/2r を思い出します。
正方形の一辺を r とします。
点 Q,S までの距離は r
点 R までの距離は √2r です。
・電流 Q により
大きさ I/2πr、向き 「→」…(1)
・電流 S により
大きさ 2I/2πr、向き「↑」…(2) の磁界が発生します。
※向きは右ねじの法則からわかります。右手親指を電流の向きに合わせた時に、残り 4 本の指の流れが磁界の向きと対応します。
・電流 R により
大きさ 2I/(2π × √2r)、向き「↙️」の磁界が発生します。斜めだとわかりにくいので、真左と真下に分解するとよいです。
大きさ I/2πr、向き 「←」…(3) と
大きさ I/2πr、向き 「↓」…(4) に分解できます。
(1) ~ (4) のベクトル和を考えれば
↑ 方向だけ残ります。㋑ が妥当です。
以上より、正解は 2 です。

コメント