問 題
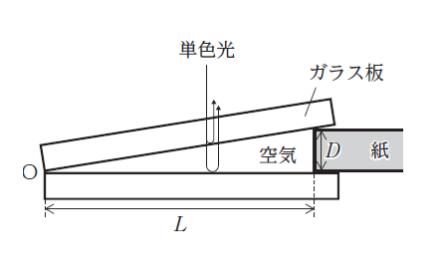
図のように、 2 枚の平面ガラス板を一端 O で密着させ、O より距離 L 離れたところで 2 枚のガラス板の間の距離が D になるようにもう一端に薄い紙を挟んで、くさび形の空気層をつくった。真上から波長 λ の単色光を当て、上側のガラス板の下面で反射した光と下側のガラス板の上面で反射した光を真上から観測すると、これらの光が干渉して、明暗の縞模様が生じた。
このとき、O から数えて 2 番目の明線と O との距離として最も妥当なのはどれか。なお、屈折率の小さい媒質中を進んでいた光が屈折率の大きい媒質との境界面で反射するとき、その位相は半波長分だけ変化する。

解 説
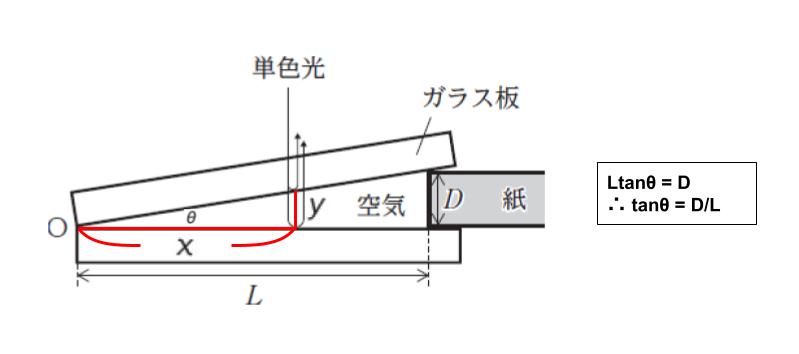
2 枚のガラス板のなす角を θ とおきます。L tan θ = D なので、tan θ = D/L です。
単色光の 2 つの反射光の光路差は、2 枚のガラス板の 隙間を y とすれば 2y です。o から 下面ガラス板での反射した点までを x とおくと x tanθ = y なので、y = xD/L です。
光路差が ちょうど波長の整数倍、λ、2λ… mλ となると強め合う → 明るくなる → 明線が基本です。
本問では「なお…」という部分から反射により 半波長ずれます。これをふまえると、明線ができるのは、光路差 2y が 0.5 λ、1.5λ… (m + 1/2) λ となる所です。 O から数えて 2 番目の明線と O との距離は、光路差 2y = 1.5λ となる所です。
2y = 2xD/L = 1.5λ を x について解けば
x = 0.75 × Lλ/D です。0.75 = 3/4 です。
以上より、正解は 2 です。
類題 国家一般職 化学 H30 no7
https://yaku-tik.com/koumuin/h30-kagaku-07/

コメント