問 題
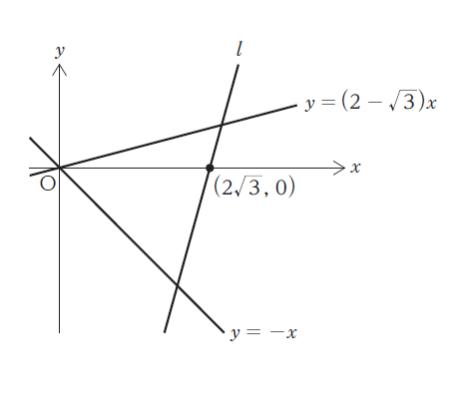
図のように、xy 平面上において、直線 y = (2 – √3) x と直線 y = – x があり、ここに点 (2√3、0) を通る直線 l を加えて、これらの 3 直線で囲まれる領域を正三角形とした。このとき、直線 l の傾きはいくらか。
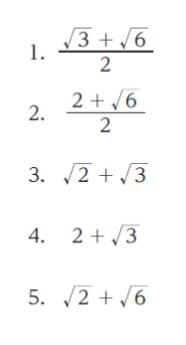
解 説
√3 ≒ 1.73 は基礎知識です。これをふまえてできるだけ正確に図を書き、傾き 3 はやや越えてそう という点から選択肢 4 or 5 には絞りたい問題です。
また、見た目から x 軸と 直線 l が成す角は 75° で、tan 75° を覚えていれば、正解は 4 でいいような気もします。
点 (2√3,0) を A とおきます。また、y = -x と 直線 l の交点を B とします。点 B から x 軸に垂線の足を引き、x 軸との交点を C とします。
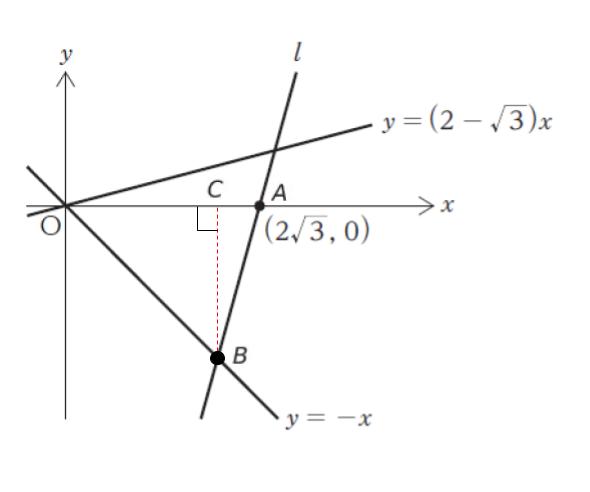
△ OBC が直角二等辺三角形なので、∠ OBC = 45° です。正三角形の 角は 全て 60° なので∠CBA = 60° – 45° = 15° とわかります。そのため、直線 l の傾きは tan 75° です。
tan の加法定理を覚えていればよいのですが、忘れていた場合は「75° の三角比」について、以下のように求めるのがおすすめです。
「辺の比が 1:2:√3 の直角三角形を書く
→ 辺の比 2 の辺をコピーして、√3 の辺を延長させるようにくっつける
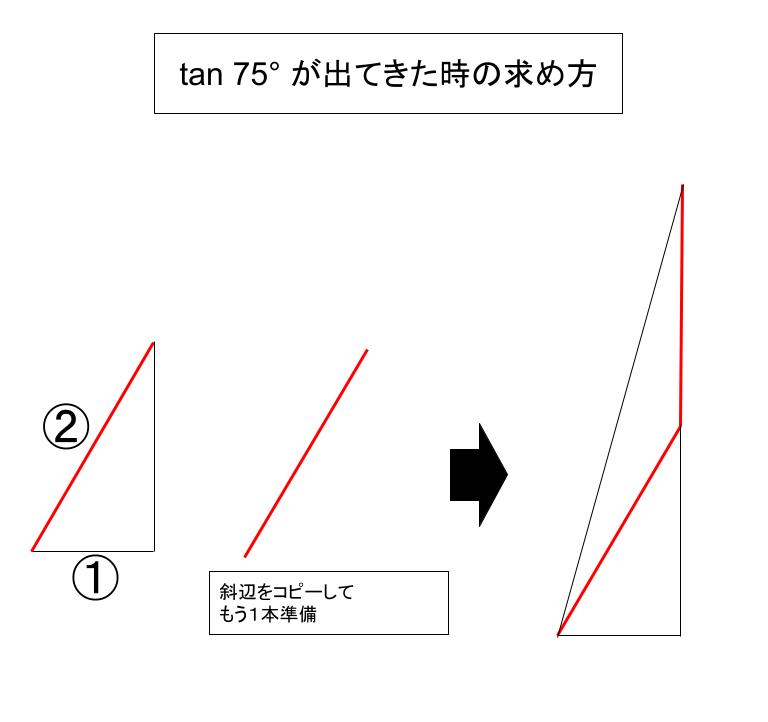
→ 90°、75°、15° の直角三角形ができる。
横に 1、縦に 2 + √3 なので、tan 75° = 2 + √3 とわかる」
※ cos 75°、sin 75° については、三平方の定理で斜辺を求めればよいです。二重根号が外せない場合は、答えを覚えてもよいのかなと思います。
以上より、正解は 4 です。

コメント