問 題
表が赤、裏が白であるコインと、箱があり、初め、箱の中には赤玉と白玉が 1 個ずつ入っている。このとき、次の操作を行う。

操作の結果、箱の中の玉が 0 個になった場合は操作を終了し、それ以外の場合は操作を最大で 6 回繰り返すものとするとき、操作の回数の期待値はいくらか。ただし、コインの表が出る確率と裏が出る確率は等しいものとする。
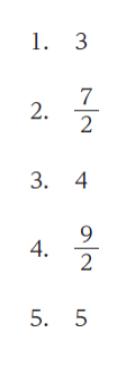
正解.2
解 説
表が真っ赤なコインってかっこいいなと思った問題です。期待値の問題では、変数 X と、その変数 X となる確率 P(X) の表を書くのが基本です。
1回目の操作では
確実に箱から玉を 1 つ取り出します。操作が終了する確率は 0 です。
次に、2回目の操作で
1/2 の確率で 箱の中の玉が 0 になります。1/2 の確率で初めの状態に戻ります。
操作が続いているのであれば
3回目の操作では
確実に箱から玉を 1 つ取り出します。
4回目の操作で
1/2 の確率で 箱の中の玉が 0 になります。1/2 の確率で初めの状態に戻ります。
4 回目の操作で終了する確率は
「操作が続いている確率」 1/2 ×
「4回目の操作で箱の中の玉が 0 になる確率」1/2 なので、1/4 です。
5回目の時点で操作が続いているのであれば
6回目で操作が必ず終了になります。この確率は 1 です。
6回目の操作で終了する確率は
「操作が続いている確率」 1/2 × 1/2 なので、1/4 です。
以上をまとめると
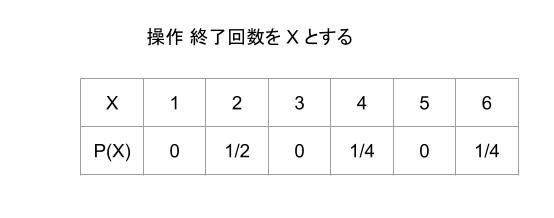
従って、求める期待値は
1/2 × 2 + 1/4 × 4 + 1/4 × 6 = 7/2 です。
以上より、正解は 2 です。

コメント