問 題
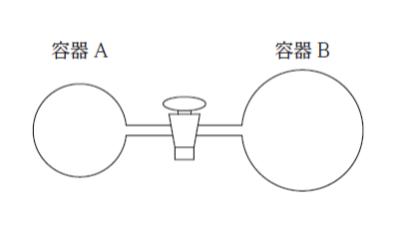
図のように、3.00 L の容器A と5.00 L の容器B がコックの付いた細管で連結されている。
コックを開けた状態で、一定温度で 0.800 mol の理想気体を満たし、コックを閉じた。容器A 内の気体については 300 K、 容器 B 内の気体については 500 K に保ち、その後、コックを開けたところ、容器A 及びB 内の気体の温度は変化せず、気体の圧力が一定となった。
このとき、コックを開ける操作前後での容器 A 内の気体の物質量変化に関する記述として最も妥当なのはどれか。ただし、容器の熱膨張及び細管の容積は無視できるものとする。
1. 0.200 mol 減少
2. 0.100 mol 減少
3. 変化なし
4. 0.100 mol 増加
5. 0.200 mol 増加
解 説
理想気体なので、状態方程式 pv = nRT を思い出します。n = pv/RT です。
まず、コックを開けた 状態で 0.800 mol の理想気体を満たし、コックを閉じた所では、p,T は容器 A,B で違いがありません。つまり v の比率がそのまま物質量の比率となります。容器 A の体積:容器 B の体積 = 3:5 なので、0.8 mol が 3:5 で分配されます。つまり、容器 A に 0.3 mol、容器 B に 0.5 mol 気体があります。
次に、温度がそれぞれ 300K、500K とした後、コックを開けます。圧力は一定になったということなので、各容器の気体に共通の圧力を P とします。
容器 A に注目すると
nA = (P × 3)/R × 300…(1) です。
容器 B に注目すると
nB = (P × 5)/R × 500…(2) です。
(1) と (2) の右辺は約分すると 等しくなります。つまり、nA = nB です。nA + nB = 0.800 mol なので、nA = 0.4 mol とわかります。
容器 A 内の気体の物質量は
0.3 mol → 0.4 mol なので「0.100 mol 増加」です。
以上より、正解は 4 です。
類題 H30 no3
https://yaku-tik.com/yakugaku/km-30-03/

コメント