問 題
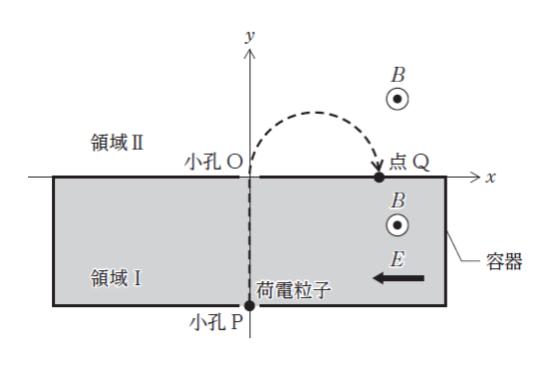
図のように、真空中に、容器内の領域Ⅰ及び容器外の領域Ⅱがあり、容器の小孔 O を原点とし、小孔 P が y 軸上にあるように xy 座標をとる。領域Ⅰには x 軸の負の向きに大きさ E の一様な電界と、紙面の裏から表の向きに磁束密度の大きさ B の一様な磁界があり、領域Ⅱには領域Ⅰと同じ磁界のみがある。
いま、電気量 q(q > 0)、質量 m の荷電粒子が、ある速さ v で y 軸の正の向きに小孔 P から領域Ⅰに進入したところ、荷電粒子は y 軸に沿って直進して小孔 O を通過した後、x 軸上の点 Q に到達した。このとき、v と点 Q の x 座標の組合せとして最も妥当なのはどれか。ただし、重力の影響は無視できるものとする。
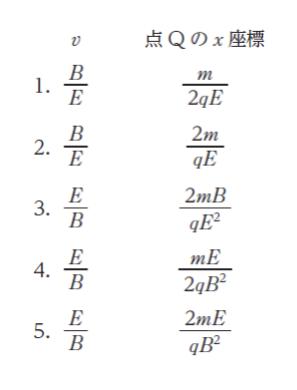
解 説
全く手がつけられなくても、具体的に考えて選択肢を 1 つでも消しましょう。本問では B が大きければ、穴を出た瞬間に強く曲がるため「B が大きいほど x が小さくなる」選択肢が答えと推測されます。つまり、正解は 4 or 5 です。ぜひ、この 2 択まで持っていきましょう。
ーーー
「磁界から電荷(荷電粒子)が受ける力」ときたら、ローレンツ力の公式 f = qvB…(1) です。また、一様な電界から 荷電粒子が受ける力は F = qE…(2) です。(1) と (2) が釣り合うから、領域Ⅰでは真っすぐ進んでいます。従って qvB = qE ∴ v = E/B です。正解は 3 ~ 5 です。
領域Ⅱでは、半径 x/2 の等速円運動をしています。領域Ⅱでは、ローレンツ力のみを受けるため、これが遠心力と等しくなります。
等速円運動の遠心力公式:F = mv2/r より
qvB = mv2/(x/2) です。x について解けば
x = 2mv/qB です。ここで先程もとめた v = E/B を代入すれば
x = 2mE/qB2 となります。
以上より、正解は 5 です。

コメント