問 題
虹に関する次の記述の㋐、㋑、㋒に当てはまるものの組合せとして最も妥当なのはどれか。
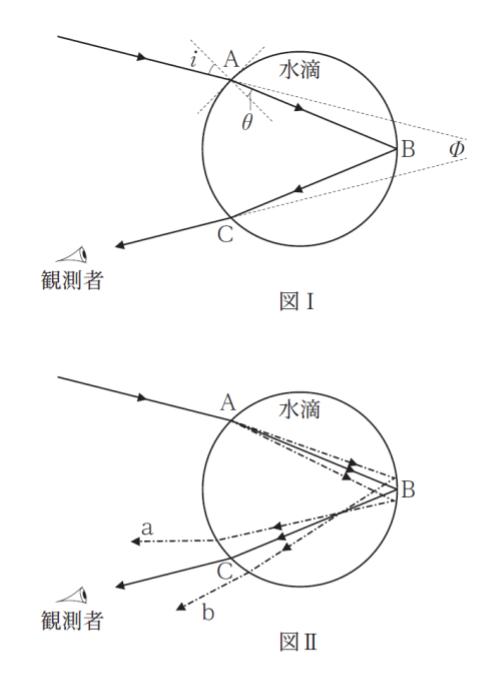
「虹は、雨が降った後など空気中に広く水滴があるときに、太陽を背にすると見えることがある。その原理について、図Ⅰ、Ⅱのような完全な球とみなせる水滴に、ある波長 λ の可視光が空気中から入射するモデルを用いて考える。ただし、可視光の経路は全て同一平面内にあるものとする。
図Ⅰのように、ある波長 λ の可視光が空気中から水滴に、点A において入射角 i で入射したとき、入射した光は屈折角 θ の方向に屈折し、点 B で一部が反射する。反射した光は点 C で再び屈折し、空気中に出る。水滴に入射した光と、空気中に出てきた光のなす角 Φ を、i、θ を用いて表すと ㋐ となる。
太陽を背にした観測者からは、空気中に広くある水滴から出てくる光が円弧状に見える。また、入射する光の波長が短いほど、水滴の屈折率は大きくなる。そのため、様々な波長の光から構成される太陽光は水滴内で分散し、波長が λ よりも短い光は図Ⅱ中の ㋑ 側の進路をとる。よって、紫色は、赤色よりも虹の円弧の ㋒ に見える。」
㋐ ㋑ ㋒
1. 4θ – 2i a 内側
2. 4θ – 2i a 外側
3. 4θ – 2i b 外側
4. 2θ – i a 内側
5. 2θ – i b 外側
解 説
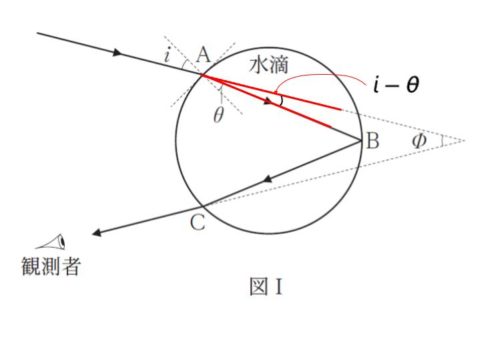
㋐ ですが、まず、入射角と屈折角の差 i – θ が上図の赤で示した角の部分です。
次に、円の接線に対する垂線を延長し、中心と B を結んだ補助線を引きます。「円が出てきたら中心と特徴的な点をつないでみよう」という試験全般の戦術になります。

角Φのある点を、そのままΦと呼びます。四角形 AΦCB に注目します。
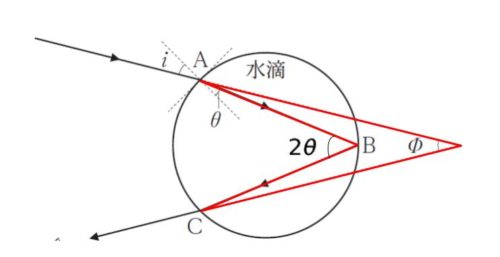
対称性から、∠A = ∠C = i – θ です。また、∠B は 2θ です。四角形の内角の和が 360° なので
(360 – 2θ) + (i – θ) + (i – θ) + Φ = 360 です。
∴ Φ = 4θ – 2i です。正解は 1 ~ 3 です。
図 Ⅰ が波長 λ の場合のモデルです。波長が短いほど屈折率が大きくなるのだから、よりぐいっと曲がっている方ということです。㋑ は a とわかります。正解は 1 or 2 です。
㋒ は、見たことのある虹を思い出してもよいかもしれません。内側が紫です。
以上より、正解は 1 です。

コメント