問 題
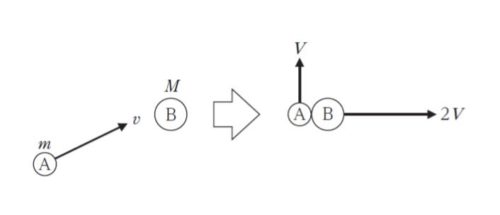
図のように、滑らかな水平面上において、質量 m の小球 A を、静止している質量 M の小球 B に速さ v で衝突させたところ、A の速さは V、B の速さは 2V となり、A とB は互いに垂直な方向に運動した。このとき、二つの小球の質量の比 M/m はおよそいくらか。ただし、A とB の衝突は弾性衝突とする。
1. 1/2
2. 1
3. √2
4. 3/2
5. 2
正解.2
解 説
衝突なので、運動量保存則を思い出します。運動量とは、質量×速度のことです。縦方向、横方向それぞれで保存されます。衝突前の A の進んでいる方向と真横のなす角を θ とします。
また「弾性衝突」というキーワードがあるため、運動エネルギーも衝突の前後で保存されます。運動エネルギーは mv2/2 です。
運動量保存(縦)より
mvsinθ = mV ∴vsinθ = V ・・・(1)です。
運動量保存(横)より
mvcosθ = 2MV です。求めたいのが M/m なので、両辺を m で割ってみて、(1)代入すると
M/m = cosθ/2sinθ と表すことができます。
一方、運動エネルギー保存から
mv2/2 = mV2/2 + M(2V)2/2 です。やはり m で両辺を割ってみて、2 を両辺にかけると
v2 = V2 + M/m × (4V2) となります。(1)を代入すれば
M/m = (1-sin2θ)/4sin2θ です。ここで、1-sin2θ = cos2θ です。
以上より
M/m は、2 乗しても値が変わらないとわかります。
※(cosθ/2sinθ)2 = cos2θ/4sin2θ です。
2乗しても値が変わらない値を探します。
選択肢 より、正解は 2 です。

コメント