問 題
配列要素a[1]、a[2]、…、a[N](N≧ 2)から成る配列a が定義され、それぞれの配列要素に整数データが入っている。
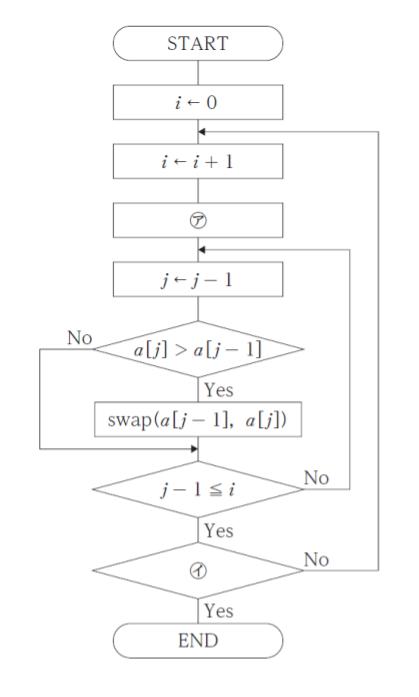
図は、このN 個のデータについて、最後の配列要素内のデータから隣接する配列要素内のデータ(a[N] とa[N -1]、a[N -1]とa[N- 2]、…)の大小を順番に比べていき、データが降順(大きいものから小さいものの順)になっていなければそれらのデータを入れ替える処理を繰り返すことで、配列要素内の全てのデータを降順に並べ替えるフローチャートである。
ここで、swap(a[ j- 1]、a[ j ])は、二つの配列要素a[ j – 1]、a[ j ] 内のデータを入れ替える操作を表している。例えば、a[ j-1]=1、a[ j ]= 2 に対してswap(a[ j- 1]、a[ j ])を実行すれば、a[ j-1]=2、a[ j ]=1 となる。
図の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのは次のうちではどれか。
㋐ ㋑
1.j ← N i ≧ N- 1
2.j ← N i < N
3.j ← N +1 i ≧ N-1
4.j ← N +1 i < N- 1
5.j ← N +1 i < N
解 説
具体的で簡単な配列を考え、各選択肢を判断するとよいです。
一例として、a[1] = 1, a[2] = 2 を考えます。チャートを読み終わった時に、データが降順、つまり、a[1] = 2, a[2] = 1 となっていればよいとわかります。
㋐ の所までチャートを読んでいくと
(i,N) = (1,2) の状態で、㋐ になります。 j ← N が正解と仮定すると
(i,j,N) = (1,2,2)
(i,j,N) = (1,1,2) となって、条件 a[1] > a[0] となりますが、a[0] は存在しません。
従って、㋐ は j ← N + 1 とわかります。正解は 3 ~ 5 です。
j ← N + 1 として、続きを読んでいきます。
(i,j,N) = (1,2,2) で、a[2] > a[1] は yes です。swap(a[1],a[2]) で、値は降順となりました。これでチャートをあっさり終われれば OK です。
次の条件分岐は j-1 が1,i も1 なので yes です。
そして ㋑ となります。
i = 1, N = 2 なので、ここで yes になるのは、i ≧ N-1 だけです。
以上より、正解は 3 です。

コメント