問 題
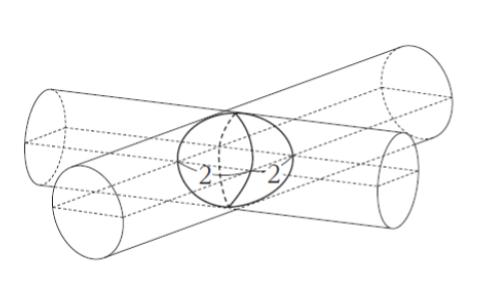
図のように、底面の直径が 2 で長さが十分に長い二つの直円柱を、それらの中心軸が直交するように配置した。このとき、二つの直円柱の共通部分の体積はいくらか。
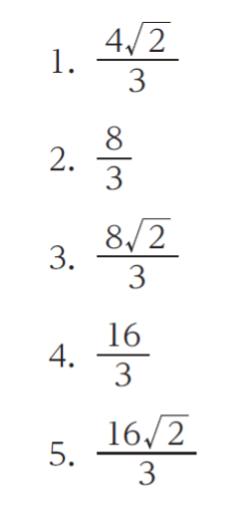
正解.4
解 説
なつかしー!解いたことあるー、という人もいるかもしれませんが、切断して積分とかしてると時間足りない、久しぶりで計算ミスしてあわない、といった可能性が高いです。選択肢が、そこそこ間があいている数が並んでいるため、大雑把な体積評価がよいと思われます。
求めたい体積は「直径2の球より少し大きそう」です。直径2の球=半径1の球なので、体積は 4π/3 です。π は 3 より少し大きいので、半径1の球の体積は、4 より少し大きいとわかります。それよりもさらに少し大きいため、4~6程度と評価できます。
選択肢 1 ~ 3 は、値が 4 以下なので、誤りと考えられます。
※√2 ≒ 1.4 なので、8√2/3 ≒ 11.2/3 < 12/3 です。12/3 = 4 です。
選択肢 5 ですが
16√2/3 ≒ 22.4/3 となり、7 よりも大きい値です。少し大きすぎではないかと考えられます。
以上より、正解は 4 です。

コメント