国家公務員総合職（化学・生物・薬学）R1年 問11解説

　問 題　　　　　

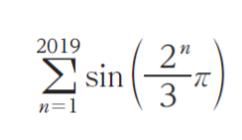
はいくらか。

1.　ー√3/2
2.　ー1/2
3.　０
4.　1/2
5.　√3/2

 

 

 

 

 

　解 説　　　　　

大きな数が出てきたら、具体的に 0,±1 などから値を求め、規則性がないかを考えます。

n = 1 までの和であれば、sin (2π/3) = √3/2 です。
n = 2 までの和であれば、sin(2π/3) + sin (4π/3) = √3/2 ー √3/2 = 0 です。
n = 3 までの和であれば、sin(2π/3) + sin(4π/3) + sin(8π/3) = √3/2 ー √3/2 + √3/2 = √3/2 です。
n = 4 までの和であれば、√3/2 + sin(16π/3) = √3/2 ー √3/2 = 0 です。

どうも n が奇数なら、結局和が √3/2、偶数であれば 0 になるようです。2019 は奇数なので、√3/2 と考えられます。

以上より、正解は 5 です。