問 題
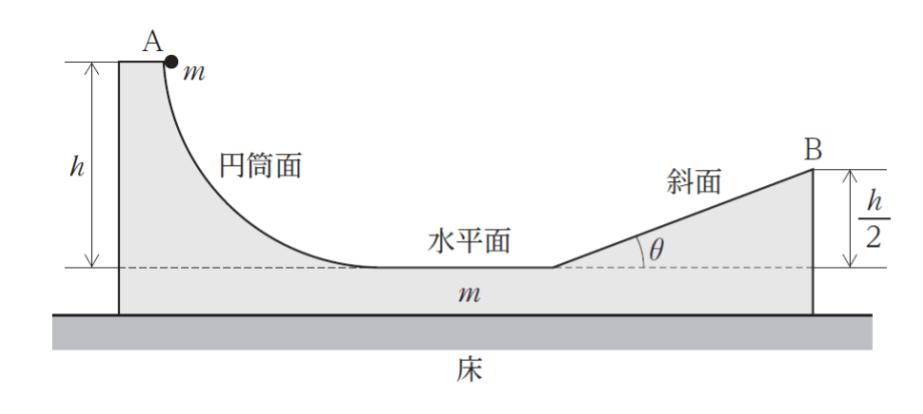
図のように、滑らかな円筒面、滑らかな水平面、水平面と角 θ(0° < θ < 90°)をなす滑らかな斜面を、それぞれ滑らかにつなげた質量 m の台が、水平で滑らかな床の上に静止した状態で置かれている。
いま、円筒面上の左端 A から質量 m の小物体を静かに放したところ、台が水平方向に滑り出すとともに、小物体は台上を滑り、斜面上の右端 B から飛び出した。なお、台から見ると、小物体は水平面と角 θ をなす向きに B から飛び出すように見える。このとき、B を通過する瞬間の小物体の床に対する水平方向の速さとして最も妥当なのはどれか。
ただし、A、B の水平面からの高さをそれぞれ h、 h/2 、重力加速度の大きさを g とする。また、
台の底面は常に床と接しており、空気の影響は無視できるものとする。
解 説
試験本番では、時間を相当消耗してしまいかねず、できたら避けたい問題という印象です。
本問題では、台も動くという点が特徴です。台の速度も考えると変数が1つ増えて、力学的エネルギー保存則だけでは 球の速さを選択肢のように θ、g、h だけでは表せません。そのため他に式立てれる関係は・・・と考えます。運動量保存則を考えます。
「台から見ると θ 方向に飛び出す」とあるので、「台から見て 速度 v」 で球が B から飛び出したとします。「台から見た水平方向の速さ」は v cos θ です。問われているのは「床に対する速度」です。床から眺めているイメージで見た時、台が動いているため、これを考慮しなければいけません。
球が B から飛び出す時、台が 速度 V で動いているとします。すると、床から見た(要するに、外から眺めてるイメージ)球の水平方向の速さは V + vcosθ となります。
運動量保存則から、A 地点にいる時、球、台共に動いてないから運動量0です。B 地点にいる時、球の運動量は m × (V + vcos θ)、台の運動量は mV です。従って
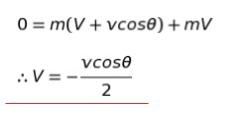
とわかります。
後は力学的エネルギー保存則で式を立てます。
始めは球の位置エネルギーが mgh、運動エネルギー 0 です。
球が飛び出す時、球の位置エネルギーが mgh/2 です。飛び出す時の垂直方向の速度は vsin θ です。そのため、床から見た球の飛び出す速さの 2 乗が『(V+vcosθ)2 + vsinθ2』と表されます。そして、V は先程の運動量保存則から -vcos θ/2 とわかっています。さらに、台の持つ運動エネルギーが mV2/2 です。こちらの V も -vcos θ/2 になります。従って

求めたいのは水平方向 V + vcosθ = vcosθ/2 なので、cosθ/2 をかければ
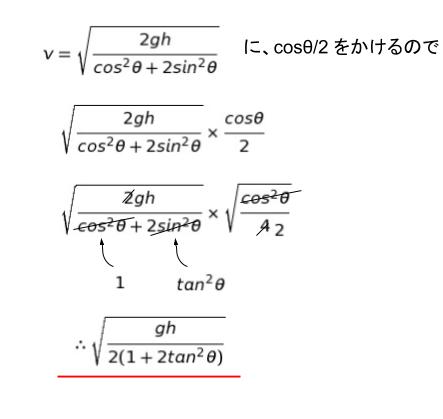
以上より、正解は 1 です。

コメント