問 題
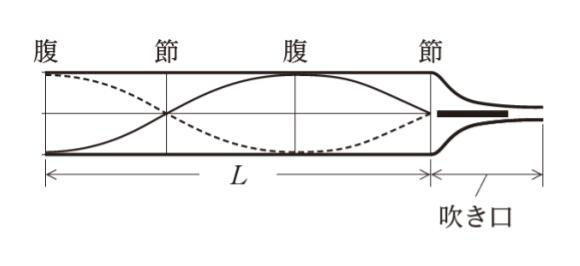
長さが変えられる笛がある。この笛の管体は、吹き口がある方の端は閉口、もう一方の端は開口とみなすことができる。
気温300 K の部屋でこの笛を吹いたところ、管体の長さ L が27.0 cm のとき、図のような定常波が発生し、周波数 f の音が響いた。気温 270 K の部屋で L を調節してこの笛を吹いたところ、再び図のような定常波が発生し、同じ周波数 f の音が響いた。このときの L はおよそいくらか。ただし、気体中を伝わる音波の速さv〔m/s〕は、気体の密度をρ〔kg/m3〕、比熱比を c、圧力を p〔Pa〕とすると
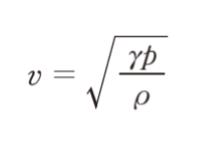
で表され、c は一定とみなせるものとする。また、 10 =3.16 とし、さらに、開口端補正は無視
でき、空気には理想気体の状態方程式が成り立つものとする。
1. 24.3 cm
2. 25.6 cm
3. 27.0 cm
4. 28.6 cm
5. 30.0 cm
解 説
L = 27.0 cm の時、図の波における波長を λ とすれば、27.0 = 3λ/4 です。λ = 36.0 cm とわかります。
波の基本式 v = fλ です。問題文に与えられた v = √γp/ρ を用いて、300K、L = 27.0 cm における 波の速さを v1 とすれば
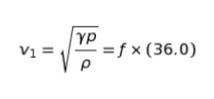
と表すことができます。
次に、270K の場合を考えます。温度が 9/10 倍になっています。理想気体の状態方程式 pv = nRT を考えると、本問における V は部屋の体積であり、ほぼ定数とみなせる状況です。従って、温度が 9/10 倍なら、p も 9/10 倍です。9p/10 とおきます。270 K において、波の速さを v2 とすれば
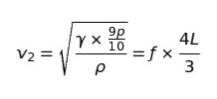
と表すことができます。√10 = 3.16 を利用し、式を変形します。

従って、f × 4L/3 = 3/3.16 × f × 36.0 となります。これを L について解けば
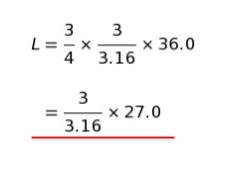
です。
式に注目すれば、L は、27 より小さく、さらに 分数部分を 3/3.15 と近似すれば 100/105 なので、27 × 105/100 について考えれば、27 から大体 5% 程度しか小さくなりません。27 の 5% が 1.35 なので、大体 25.6 ~ 25.7 と概算できます。選択肢から近い数値を選べば 25.6 が妥当です。
以上より、正解は 2 です。

コメント