問 題
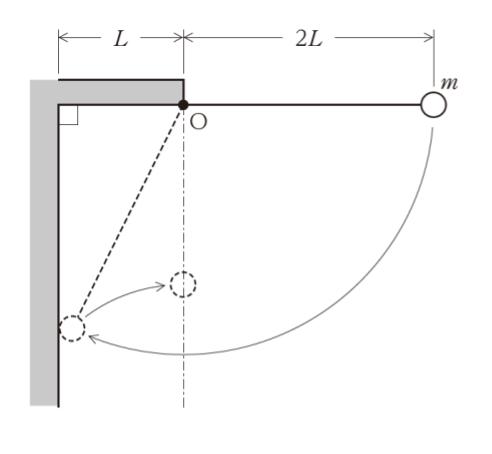
図のように、鉛直で滑らかな壁の張出し部の先端下縁の点 O に長さ 2L の糸を取り付け、糸の他端には質量 m の小球を取り付ける。糸を張った状態で点 O と同じ高さから小球を静かに放したところ、小球は壁に衝突し、糸がたるんだ。跳ね返った小球が、糸がたるんだ状態のまま点 O の鉛直線上で最高点に達したとき、壁と小球の間の反発係数として最も妥当なのはどれか。
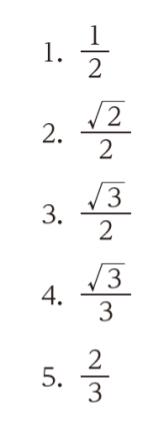
正解.5
解 説
L は何でもいいので、1 とおきます。
まず、壁に衝突する直前の速さを、力学的エネルギー保存則より求めます。衝突した部分の高さは、(2-√3) です。
2mg = (2-√3)mg + mv2/2 を解いて
v2=2√3g です。二重根号はいやなので、とりあえずこのままにしておきます。
水平成分、垂直成分を vx , vy とおけば
vx = v × cos30°、vy = v × sin30° です。そして、壁との衝突後は、水平方向だけ、反発係数をかけた速度になります。(下図参照)
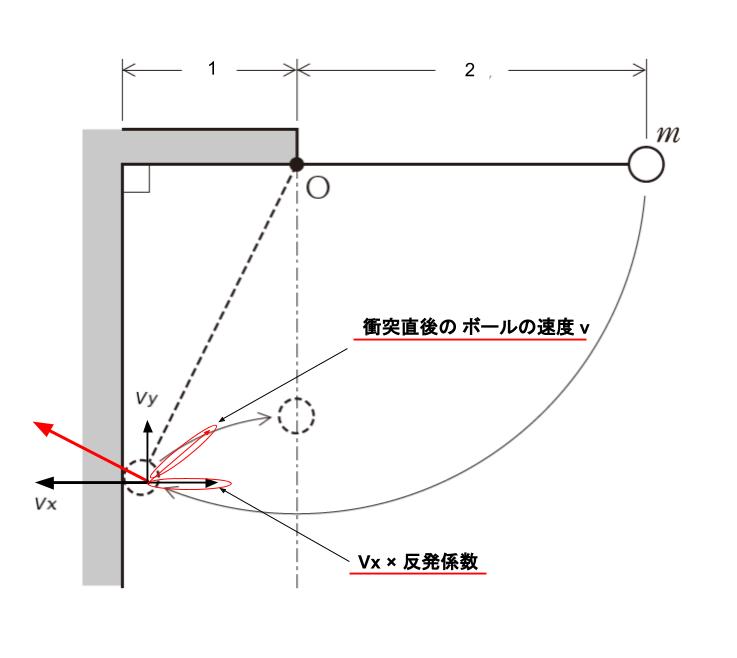
「ちょうど O の鉛直線上で最高点」というのは、「壁に反射した時の初速により、ボールを斜めに投げ上げた」と考えれば『水平方向に 1 進んだ時、vy – gt = 0』と解釈することができます。
初速 vy で鉛直投げ上げした時の最高到達時間 t = vy/g です。反発係数を e とおけば、水平方向は等速直線運動なので、水平方向に e × Vx × (vy/g) 進みます。計算すると以下のようになります。

以上より、正解は 5 です。

コメント