国家公務員総合職（化学・生物・薬学）H28年 問14解説

　問 題　　　　　

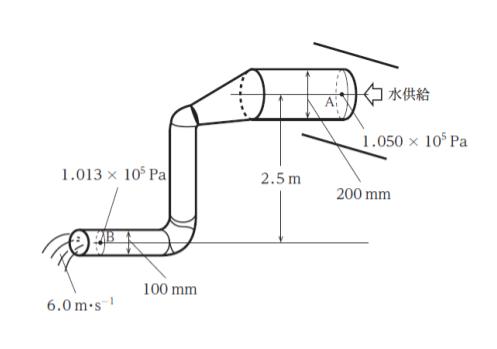
図のように、水が 6.0 m・s^-1 の速度で、内径 100 mm の水平直管内から大気中に放出されている。この流出管には、流出口の位置から 2.5 m の高さに、内径 200 mmの水平直管が接続されており、ここから水が供給されている。

内径 200 mm 管のある断面 A の静圧は 1.050 × 10⁵ Pa であり、流出口付近の断面 B の静圧は 1.013 × 10⁵ Paであった。AB 間における水 1 kg 当たりのエネルギー損失はおよそいくらか。ただし、重力加速度の大きさ g を 9.8 m・s^-2 とする。また、水の密度 ρ₀ を 1.0 × 10³ kg・m^-3 とし、ベルヌーイの定理、すなわちエネルギー損失がなければ、

が成り立っているものとする。

1.　3.9 J・kg^-1
2.　11 J・kg^-1
3． 17 J・kg^-1
4． 37 J・kg^-1
5． 45 J・kg^-1

 

 

 

 

 

　解 説　　　　　

連続の式 Q = Av です。

内径が 2 倍になると、断面積が 4 倍になります。流速は 1/4 倍です。これにより、点 B の流速が 6.0 m/s だから、点 A の流速は 1.5 m/s とわかります。

点 A、B に対してベルヌーイの定理を適用し、数値を代入します。g ≒ 10 とします。また、点 A → 点 B により失われる損失水頭を h とします。

左辺が 1.125 + 25 + 105、右辺が大体 18 + 101 + h となります。h ≒ 12 です。選択肢から一番近いものを選ぶと 11J/kg です。

以上より、正解は 2 です。