国家公務員総合職（化学・生物・薬学）H27年 問13解説

　問 題　　　　　

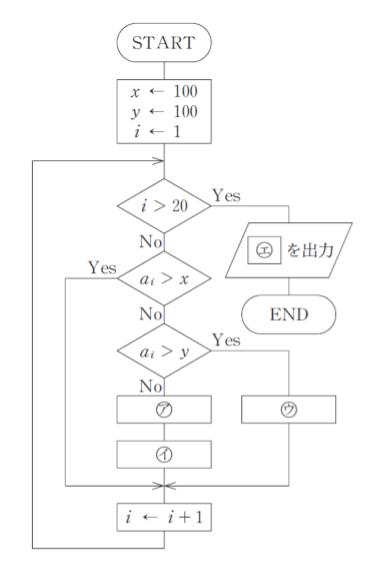
図は、100 未満の互いに異なる 20 個の正の整数 a₁, a₂, …, a₂₀ のうちから ２ 番目に小さい数を出力するフローチャートである。図の ㋐ ～ ㋓ に当てはまるものの組合せとして最も妥当なのはどれか。

㋐　㋑　㋒　㋓
1. x ← y　y ← a_ix ← a_i　x
2. x ← y　y ← a_ix ← a_i　y
3. x ← y　y ← a_iy ← a_i　y
4. y ← x　x ← a_ix ← a_i　x
5. y ← x　x ← a_iy ← a_i　y

 

 

 

 

 

　解 説　　　　　

具体的に考えます。

a₁ = 1、a₂ = 2,,,a₂₀ = 20 という 20 個の整数を考えます。2 番目に小さい数が出力されるフローチャートなので、この 20 個の時に 2 が出力されるように、図をうめていきます。

上からチャートを読んでいくと
(x,y,i) = (100,100,1)nnn で、㋐、㋑ と続きます。ここで、正解が 1 ~ 3 、つまり x ← y, y ← a_i とすると、y に a₁ 、つまり y に 1 が入ります。

この仮定の下でチャートを読み進めると
(x,y,i) = (100,1,2)ny で、㋒ と続きます。x ← a_i とすると、x に a₂  、つまり x に 2 が入ります。そしてチャートを読んでいくと、a₃ 以降すべて yes となり、x を出力すれば OK です。

ところで
㋒ のところで y ← a_i とすると、y に a₂  、つまり y に 2 が入ります。x = 100 のままなので、以降ずっと ㋒ にチャートが分岐することになり、どんどん y が増えていきます。これでは 2 を出力することができません。

一応確認のため、正解が 4,5 であったと仮定します。すると (x,y,i) = (100,100,1)nnn の次に x に a₁ 、つまり x に 1 が入ります。 すると後はずっと a_i > x になり、2 を出力することができません。4,5 は誤りとわかります。

以上より、正解は 1 です。