国家公務員総合職（化学・生物・薬学）H27年 問12解説

　問 題　　　　　

xy 平面上の動点 P(x,y) の時刻 t における位置が x ＝ 3t － 1、y ＝ －t² ＋ 2t＋ 3と表されるとき、P の速さが最小となる t はいくらか。

1. 1
2. 2
3. 3
4. 4
5. 5

 

 

 

 

 

　解 説　　　　　

具体的に考えます。

t = 0 の時、(x,y) = (-1,3)
t = 1 の時、(x,y) = (2,4)
t = 2 の時、(x,y) = (5,3)
t = 3 の時、(x,y) = (8,0)
t = 4 の時、(x,y) = (11,-5)
t = 5 の時、(x,y) = (14,-12) です。

できるだけ丁寧に図を描くと、以下のようになります。t = 1 付近が一番速さが小さいと判断できるのではないでしょうか。

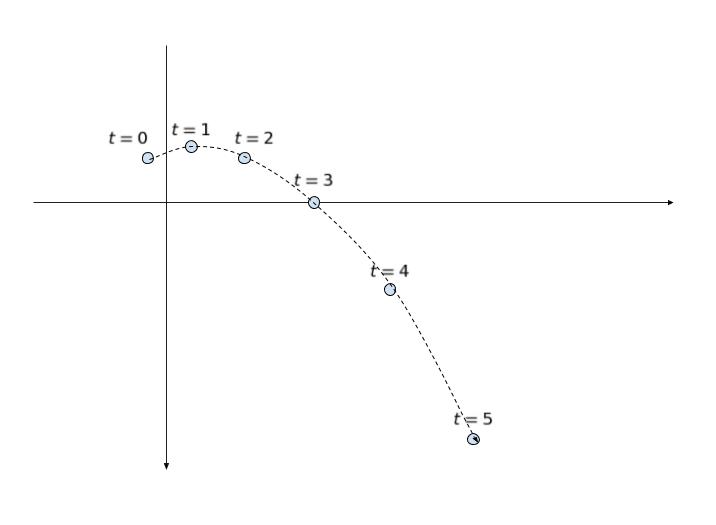
ちなみに、x,y をそれぞれ t で微分し
dx/dt = 3、dy/dt = -2t+2 となるため、x 方向には定速です。dy/dt が 0 となるため、t = 1 と考えてもよいです。

以上より、正解は 1 です。