国家公務員総合職（化学・生物・薬学）H27年 問11解説

　問 題　　　　　

xy 平面上において１次変換 f を表す行列

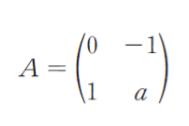
がある。f により、xy 平面上にある原点以外の任意の点 P は点 Q に移り、また、点 Q は点 R に移る。３点 P、Q、R が全て異なり、同一直線上になく、かつ、常に PQ ＝ QR となるようにa を定めるとき、a はいくらか。

1. －2
2. －√ 3
3. 0
4. 1
5. √3

 

 

 

 

 

　解 説　　　　　

点(x,y) を、(x’,y’)に移すのが変換です。x’ = ax+by、y’=cx + dy の形を一次変換といいます。行列を左からかけることで実現できます。行列 A を点に作用させると表現します。

具体的に考えます。点 A を（1,0) として、行列 A を作用させてみます。

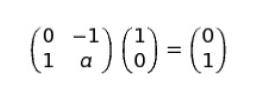
（0,1) に移ります。(0,1) に行列 A を作用させると

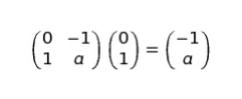
となり、(-1,a) に移ります。

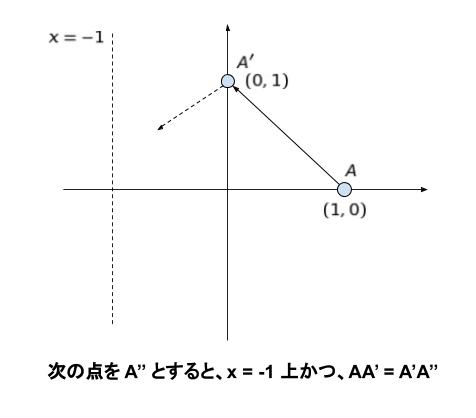
長さの条件から考えれば、a = 0 です。

以上より、正解は 3 です。

ちなみに、a = 0 の時の行列 A は、90° 回転行列を表しています。