問 題
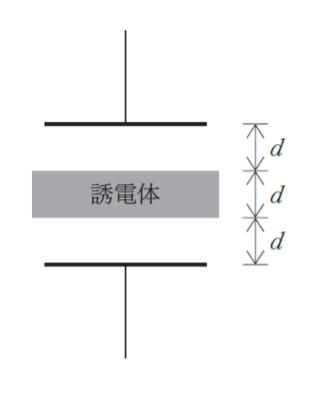
真空中に置かれた極板間隔 3d、静電容量 C の平行平板コンデンサに、厚さ d、比誘電率3の誘電体を極板から d 離れた位置に図のように平行に挿入した。このコンデンサの静電容量として最も妥当なのはどれか。
ただし、誘電体は極板より十分に大きいものとする。また、静電容量 C0 の平行平板コンデンサの極板間を比誘電率 εr の誘電体で満たすと、静電容量は εr C0 となる。
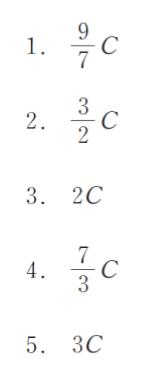
正解.1
解 説
コンデンサなので、基本公式として Q = CV、C = εS/d を思い出します。誘電体入りの場合は、誘電体入の部分とそうでない部分に分けて、コンデンサの合成とみなします。
誘電体の部分は d が 1/3 倍になり、比誘電率が 3 なので、元のコンデンサの 9 倍の静電容量です。つまり 9C です。間隙部分は、d が 2/3 倍になったので、元のコンデンサの 3/2 倍です。つまり 3/2 C です。この 2 つの合成なので、以下のようになります。
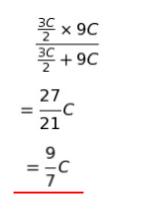
以上より、正解は 1 です。

コメント