問 題
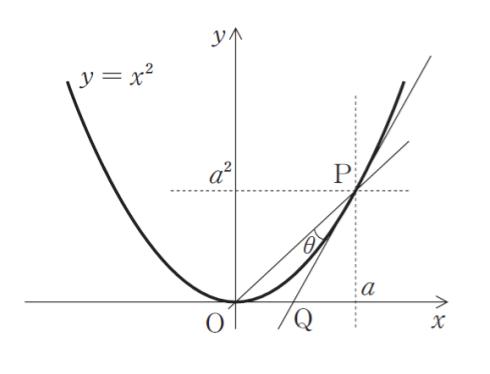
図のように、曲線 y = x2上の点P (a,a2) (a > 0) における接線と x 軸との交点を Q とする。原点を O として、∠OPQ = θ とすると、tanθ の最大値はいくらか。なお必要ならば

を用いてよい。
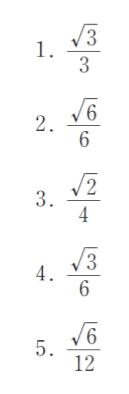
正解.3
解 説
点 P における接線の傾きは y’ = 2x より、2a です。点 (a,a2) を通るため、接線は y = 2ax – a2 と表すことができます。そのため、x 軸との交点は、y = 0 を代入することで x = a/2 とわかります。
∠QOP = X とおきます。tanX = a です。また、tan(θ + X) = 2a と表すことができます。下図参照
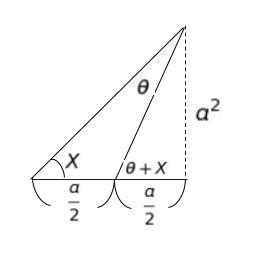
必要ならば、と与えられた式の α = θ、β = X とおけば、左辺は、tan(θ + X) = 2a です。一方、右辺ですが tan X = a なので、(a + tanθ)/(1 ー a tanθ)です。
2a = (a + tanθ)/(1 ー a tanθ)を、tan θ について解けば、tan θ = a/(2a2+1) です。f(a) = a/(2a2 + 1) とおき、a > 0 における最大値を求めればよいとわかります。
微分すれば、f’(a) = (2a2+1-4a2)/(2a2 + 1)2 = (-2a2+1)/(2a2 + 1)2 なので、a = 1/√2 の時に最大値です。tan θ = 1/(√2/2) = 1/2√2 = √2/4 です。
以上より、正解は 3 です。

コメント