国家公務員総合職（化学・生物・薬学）H26年 問11解説

　問 題　　　　　

実数 x,y が次の五つの不等式を満たすとき、x + y の最小値及び最大値の組合せとして正しいのはどれか。

 

 

 

 

 

　解 説　　　　　

まずは具体的に考えて、正解を絞りたい問題です。

x = 0 , y = 2 が明らかに不等式をすべて満たすので、x + y の最小値が 2 であることはすぐに求めることができます。正解は 1 or 2 です。

本問は、一般的には「線形計画法」の問題です。それぞれの不等式の満たす領域を考えた上で、x + y = k とおきます。y = -x + k となおせるため、傾き－１の直線を考えて、y 切片が k を表すことになります。不等式の領域が上図、一つのグラフに重ね合わせた上で、y = -x + k を点線で表したものが下図になります。

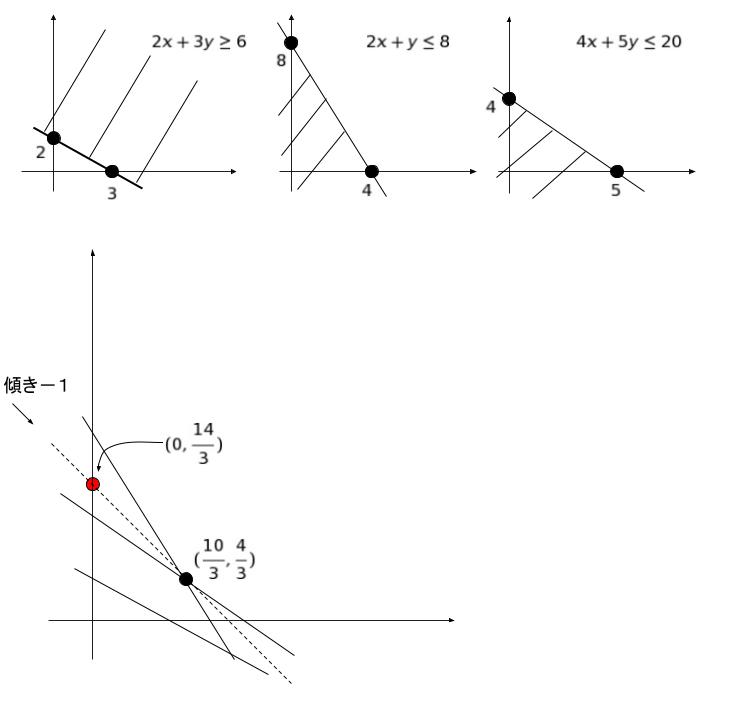
x = 10/3,4/3 の時、最大値 14/3 をとるとわかります。

以上より、正解は 2 です。