国家公務員総合職（化学・生物・薬学）H29年 問12解説

　問 題　　　　　

a、b を正の実数、e を自然対数の底とする。関数 f(x) = log_ex/x (x > 0) において、a < b、かつ、f(a) = f(b) が成り立つとき、a、b、1、e の大小関係として正しいのはどれか。

1． 1 < e < a < b
2． 1 < a < e < b
3． 1 < a < b < e
4． a < 1 < b < e
5． a < b < 1 < e

 

 

 

 

 

　解 説　　　　　

具体的に考えます。

x → 0 の時、f(x) → ー∞ です。
f(1) = 0 です。
f(e) = 1/e です。
x → ∞ の時、f(x) → 0 です。

以下のような概略図を考えることができます。x = e がちょうど頂点かどうかはわかりませんが、大体こんな感じという概略です。

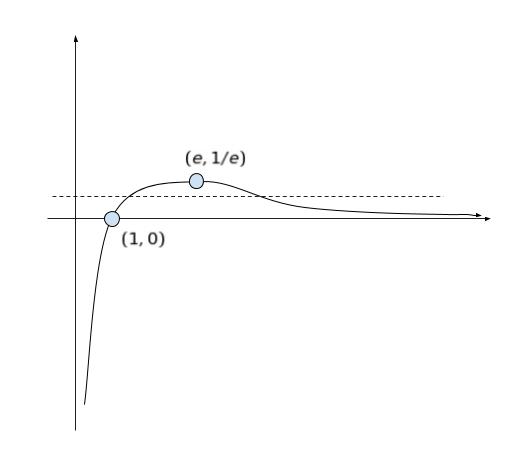
点線は、f(a) = f(b) となるような a,b を探すためにひきました。ちょうど 1 と e の間に a があり、e よりも後に b があるパターンが考えられます。1 < a < e < b で妥当と考えられます。

補足：もちろん、微分して概形をきちんと把握してから考えてもかまわない問題です。ただ、『具体的値に注目→概形把握→矛盾ない正解を選ぶ』という流れのほうが、試験一般に通用する得点力が身につくという点から、個人的には強くおすすめします。

以上より、正解は 2 です。