薬剤師国家試験 第102回 問49 過去問解説

　問 題　　　　　

下図のような拡散制御膜において、溶質分子が単位時間に透過する物質量と反比例の関係にあるのはどれか。1 つ選べ。

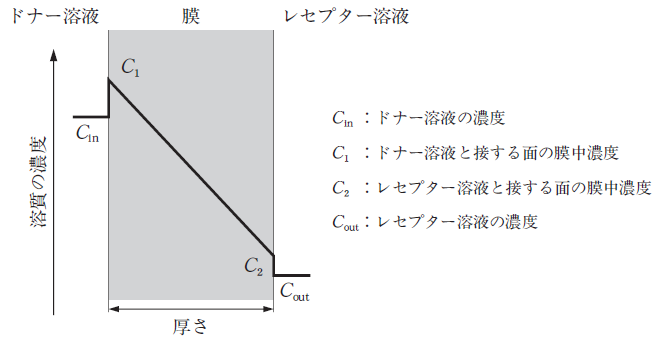
1. 溶質の膜中での濃度差 (C₁-C₂)
2. 溶質の膜中での拡散係数
3. 溶質の分配係数 (C₁/C_in)
4. 膜の厚さ
5. 膜の有効表面積

 

 

 

 

 

　解 説　　　　　

膜が厚くなればその分単位時間に透過する物質量は少なくなるだろうと考えれば、 4 を何となく選べるかもしれません。

別の考え方としては、濃度が異なる溶液を膜が隔てているということは単純拡散です。単純拡散は、 Fick の法則で表されます。Fickの法則：J = ーD dC/dx　です。J が、流束（単位時間あたりの物質の通過量）、D が、拡散係数、dC/dx は、濃度勾配のことです。これをふまえて、各選択肢を検討します。

選択肢 1 ですが
濃度差が大きくなれば、濃度勾配も大きくなります。よって、J は大きくなります。反比例の関係にはありません。

選択肢 2 ですが
拡散係数 D が大きくなると、J は大きくなります。反比例の関係にはありません。

選択肢 3 ですが
分配係数が上がるというのは、C₁/Cin の値が大きくなるということです。また、同様に C₂/Cout の値も大きくなります。分配係数を K とおけば、C₁＝KCin、かつ、C₂＝KCout　です。従って、膜中における濃度差である 「C_{1 ー} C₂」= 「K（Cin－Cout）」・・・（１）です。

Cin と Cout は溶液濃度なので定数です。つまり、（１）の式は「分配係数（K）が大きくなると、膜中における濃度差（C₁－C₂）が大きくなる」と読み取れます。濃度差が大きくなれば、濃度勾配も大きくなります。よって、J は大きくなります。反比例の関係にはありません。

選択肢 4 は、正しい記述です。
膜が厚くなれば、透過するのに時間がかかるようになると常識的に考えても納得できるのではないでしょうか。

選択肢 5 ですが
膜の有効表面積が増えるというのは、通ることができる膜の領域が増えるということです。すると、単位時間に通過する物質は当然増えると考えられます。よって、反比例の関係にはありません。

以上より、正解は 4 です。

参考　製剤学まとめ　溶解した物質の膜透過速度