問 題
肝代謝のみで消失する薬物を経口投与する場合において、以下の変化が生じたとする。血中濃度-時間曲線下面積(AUC)が2倍に上昇するのはどれか。2つ選べ。ただし、この薬物の消化管からの吸収率は100%とし、肝臓での挙動はwell-stirred modelに従うものする。
- 肝血流速度が1/2に低下した場合
- タンパク結合の置換により血中非結合形分率が2倍に上昇した場合
- 結合タンパク質の増加により血中非結合形分率が1/2に低下した場合
- 肝代謝酵素の誘導により肝固有クリアランスが2倍に増加した場合
- 肝代謝酵素の阻害により肝固有クリアランスが1/2に低下した場合
解 説
well – stirred model であるということは、肝組織及び、血管中の薬物は十分混ぜあわせられており、均一であるということです。イメージは下図のようになります。
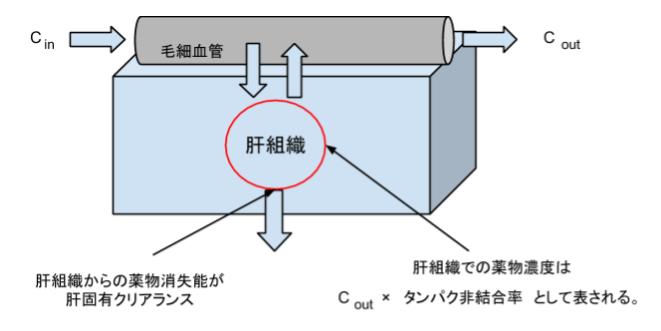
イメージを参考にすると、肝血流速度が1/2になっても血中の薬物濃度である C は変化しません。すると血中濃度-時間曲線下面積も変わらないと考えられます。よって、選択肢 1 は誤り。
さて、肝代謝のみで消失する薬物を経口投与すると、肝初回通過効果による薬物の消失をまず受けます。この消失速度は、肝固有クリアランス × 肝組織中の血中濃度で表されます。モデルから、肝組織中の血中濃度は、Cout × fu(タンパク非結合率)と表されます。よって、消失速度は CLint × (Cout ×fu)です。
消失速度が分かったので、これを時間で積分すれば「肝初回通過効果による薬物の消失量」がわかります。Cout を積分すれば、AUC なので、肝初回通過効果による薬物の消失量 = CLint × fu × AUC と表されます。
投与した薬物の量は変化していないのだから、肝初回通過効果による薬物の消失量、すなわち、上の等式の左辺は一定です。よって、CLint が半分になったり、fu が半分になると、AUC が2倍になるとわかります。ちなみに、選択肢 1 に関しても、この式に肝血流速度が関与しないことから誤りであると判断することができます。
以上より、正解は 3,5 です。

コメント