問 題
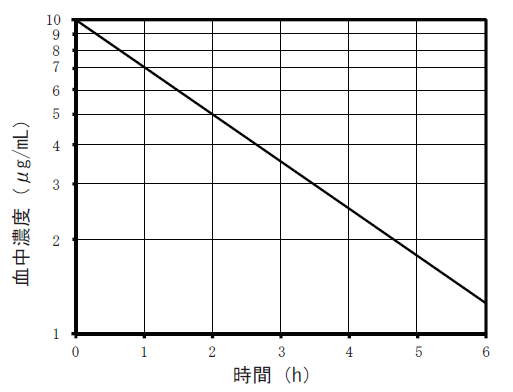
ある薬物100mgをヒトに静脈内投与したところ、下の片対数グラフに示す血中濃度推移が得られた。この薬物を50mg/hの速度で定速静注するとき、投与開始2時間後の血中薬物濃度(μg/mL)に最も近い値はどれか。1つ選べ。
- 1.8
- 3.6
- 7.2
- 14.4
- 28.8
解 説
解法1:公式を覚えていて、頑張って計算する方法
片対数グラフで、直線になっていることから、1-コンパートメントモデルと考えることができます。
次に、分布容積(Vd)、半減期(T1/2)、消失速度定数(ke)を読み取ります。グラフから、時間 0の時に血中濃度が 10 (μg/mL)で、時間 2 の時に血中濃度が 5 (μg/mL)であるから、半減期が 2h であると読み取ることができます。
又、半減期と消失速度定数は、下の式の関係で求めることができます。
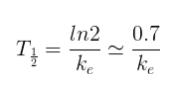
よって、半減期が 2h なので、ke は 0.35 です。
又、分布容積は Vd = X(投与量)/C0(時間 0 の時の濃度)なので、10Lと計算することができます。
さて、定速静注時の血中濃度は

と表わされるので、求める濃度は

と考えて、求める C は大体 7。以上より、正解は 3 です。
解法2:大雑把に計算する方法(推奨)
100mg 一気に注射すると、Cが最初10、2時間で半分になって5。
次に 2 回に分けて注射したとする。50mg 注射して、Cの最初は 5 となるはず。一時間経ったら、Cはよくわからないけど又 50mg 注射するから、C が 5 上がる。で、さらに一時間後を考える。
最初に注射した 50mg は2時間経過したので、C として 2.5 はあるはず。一時間後に注射した 50mg は、1 時間しか経過していないので、C として 2.5 以上あるはず。よって、Cは 2.5 + 2.5 よりも大きい値→ 5 よりも大きい値。
とすると、一気に注射するよりは、分けて注射した方が、2 時間後の濃度は高い。又、100mg 一気に注射した時の初期濃度よりも高くなることはないと考えられる。つまり、5~10 の間。
よって、正解は 3。

コメント