問 題
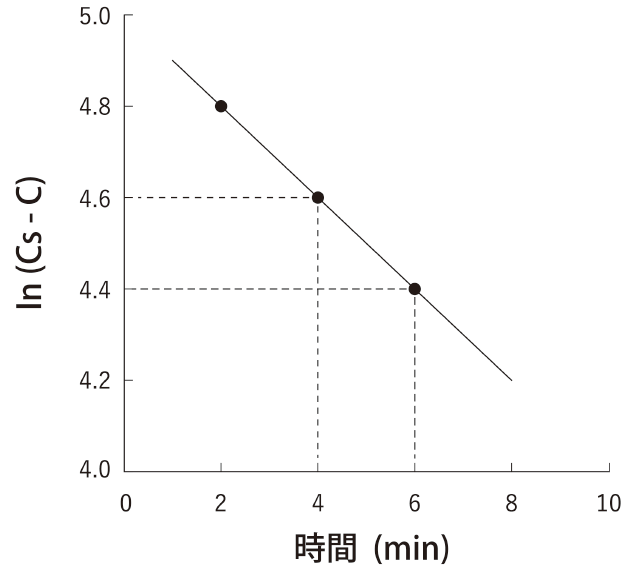
固体薬物の溶解速度を回転円盤法を用いて温度一定の条件で測定したところ、図のような結果となった。試験液中の薬物濃度 (C) が薬物の溶解度 (Cs) の半分に達するまでの時間 (min) に最も近いのはどれか。1つ選べ。
ただし、実験開始時の試験液中の薬物濃度は 0、円盤の有効表面積 (1cm2) は試験中に変化せず、溶解はシンク条件において拡散律速で進行するものとする。なお、ln2=0.69 とする。
- 3.5
- 7.0
- 10.5
- 14.0
- 17.5
正解.2
解 説
グラフ縦軸の ln(CsーC)を見て
Noyes-Whitney の式(積分型)を思い出します。

微分型だけ覚えておいて、積分はその場で行うのが暗記の負担が少なくおすすめです。微分型から積分型の導出については、本ページ下部 参考のリンク先を参照してください。
問われているのは
C = Cs/2 になる時の t です。問題文より、C0 = 0、s = 1 です。さらに、問題文におけるグラフの傾き が ー0.1 なので、k = 0.1 と読み取れます。これらを代入して、整理すれば、0.1 × t = ln2 となり、t = 10 × ln2 です。計算過程は以下の通りです。

ln2=0.69 なので、最も近いのは 7.0 です。
以上より、正解は 2 です。
類題 98-173
参考 製剤学まとめ 物質の溶解と速度

コメント