薬剤師国家試験 第107回 問176 過去問解説

　問 題　　　　　

図は、well-stirred model に基づいた肝臓からの薬物消失モデルを示したものである。このモデルに関する記述のうち、正しいのはどれか。2つ選べ。

ただし、CL_int は肝固有クリアランス、f_u は血中タンパク非結合形分率、C_in は肝臓に流入する部位における血中薬物濃度、C_out は肝臓から流出する部位における血中薬物濃度、Q_h は肝血流量とする。

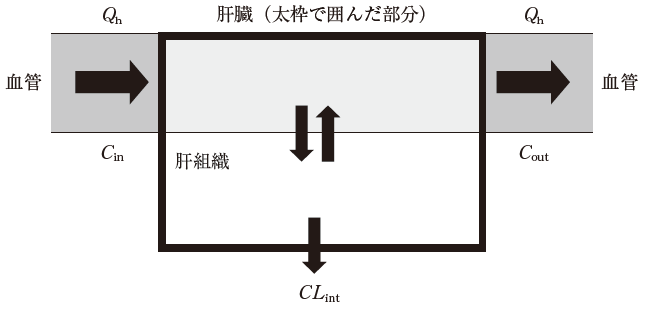
1. 肝臓中の非結合形薬物濃度は不均一である。
2. 肝組織中の非結合形薬物濃度は C_in に等しい。
3. 肝臓からの見かけの薬物消失速度は、CL_int × f_u × C_out と表される。
4. 肝臓における薬物量の変化速度は、Q_h × C_in － Q_h × C_out － CL_int × f_u × C_out と表される。
5. 定常状態における CL_int は Q_h にほぼ等しい。

 

 

 

 

 

　解 説　　　　　

血中薬物濃度ならわかるが、肝臓内の薬物濃度なんてわからない
→ 出てくる血中薬物濃度の中で、肝組織に移行できる「タンパク非結合　薬物濃度」で、わからないところは一定と仮定しよう。式で表すなら 、肝臓内についてはどこも「Cout × fu」としよう　というモデルが well – stirred model です。

選択肢 1 ですが
肝臓中の タンパク非結合薬物については、よくかき混ぜられて均一という仮定をします。「不均一」ではありません。

選択肢 2 ですが
Cout・fu です。「Cin と等しい」わけではありません。

選択肢 3 は妥当です。
薬物の消失速度は「クリアランス × 薬物濃度」です。消失速度、クリアランス、薬物濃度の関係は基礎知識です。そして、肝臓における薬物濃度は、well – stirred model において「Cout × fu」と仮定されます。

選択肢 4 は妥当です。
第一項が　入ってくる薬物量
第二項が　出ていく薬物量
第三項が　肝臓における薬物の消失量　を、それぞれ表しています。符号を「＋」にしたものが、将来的に、誤り選択肢として使われてもおかしくありません。各項の意味を　しっかりと　自分で読み取れるように確認しておきましょう！

選択肢 5 ですが
定常状態において、肝臓における薬物量の変化速度０です。選択肢 4 より、薬物量の変化速度は、Q_h×C_in － Q_h×C_out － CL_int×f_u×C_out ・・・（１）です。（１）＝０とおき、CLint = ・・・となおすと、Qh にほぼ等しいかは、fu などに依存するとわかります。（計算過程は、以下の通り）。

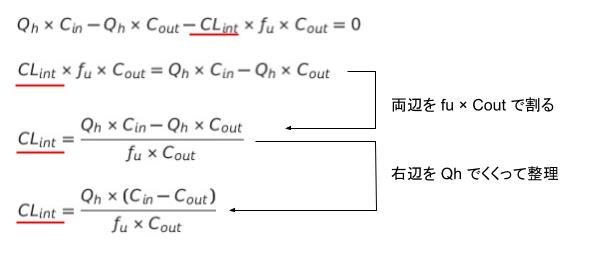
従って、選択肢 5 は誤りです。

以上より、正解は 3,4 です。

参考　薬剤学まとめ　肝クリアランス および 肝固有クリアランス